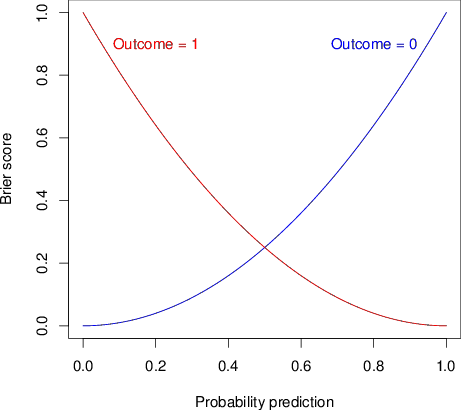
 Figure 1. Relationship between probability predictions and Brier scores in
events with binary outcomes.
Figure 1. Relationship between probability predictions and Brier scores in
events with binary outcomes.
Judgment and Decision Making, Vol. 12, No. 2, March 2017, pp. 90-103
An IRT forecasting model: linking proper scoring rules to item response theoryYuanchao Emily Bo* David V. Budescu# Charles Lewis# Philip E. Tetlock$ Barbara Mellers$ |
This article proposes an Item Response Theoretical (IRT) forecasting model that incorporates proper scoring rules and provides evaluations of forecasters’ expertise in relation to the features of the specific questions they answer. We illustrate the model using geopolitical forecasts obtained by the Good Judgment Project (GJP) (see Mellers, Ungar, Baron, Ramos, Gurcay, Fincher, Scott, Moore, Atanasov, Swift, Murray, Stone & Tetlock, 2014). The expertise estimates from the IRT model, which take into account variation in the difficulty and discrimination power of the events, capture the underlying construct being measured and are highly correlated with the forecasters’ Brier scores. Furthermore, our expertise estimates based on the first three years of the GJP data are better predictors of both the forecasters’ fourth year Brier scores and their activity level than the overall Brier scores obtained and Merkle’s (2016) predictions, based on the same period. Lastly, we discuss the benefits of using event-characteristic information in forecasting.
Keywords: IRT, Forecasting, Brier scores, Proper Scoring Rules, Good Judgment Project, Gibbs sampling.
Probabilistic forecasting is the process of making formal statements about the likelihood of future events based on what is known about antecedent conditions and the causal and stochastic processes operating on them. Assessing the accuracy of probabilistic forecasts is difficult for a variety of reasons. First, such forecasts typically provide a probability distribution with respect to a single outcome so, methodologically speaking, the outcome cannot falsify the forecast. Second, some forecasts relate to outcomes of events whose “ground truth” is hard to determine (e.g., Armstrong, 2001; Lehner, Micheslson, Adelma & Goodman, 2012; Mandel & Barnes, 2014; Tetlock, 2005). Finally, forecasts often address outcomes that will only be resolved in the distant future (Mandel & Barnes, 2014).
Scoring rules are useful tools for evaluating probability forecasters. These mechanisms assign numerical values based on the proximity of the forecast to the event, or value, when it materializes (e.g., Gneiting & Raftery, 2007). A scoring rule is proper if it elicits a forecaster’s true belief as a probabilistic forecast, and it is strictly proper if it uniquely elicits an expert’s true beliefs. Winkler (1967), Winkler & Murphy (1968), Murphy & Winkler (1970), and Bickel (2007) discuss scoring rules and their properties.
Consider the assessment of a probability distribution by a forecaster i over a partition of n mutually exclusive events, where n>1. Let pi=(pi1,…,pin) be a latent vector of probabilities representing the forecaster’s private beliefs, where pij is the probability the ith forecaster assigns to event j, and the sum of the probabilities is equal to 1. The forecaster’s overt (stated) probabilities for the n events are represented by the vector ri=(ri1,…,rin), and their sum is also equal to 1. The key feature of a strictly proper scoring rule is that forecasters maximize their subjectively expected scores if, and only if, they state their true probabilities such that ri=pi.
Researchers have devised several families of proper scoring rules (Bickel, 2007; Merkle & Steyvers, 2013). The ones most often employed in practice include the Brier/quadratic score, the logarithmic score, and the spherical score, where:
| (1) |
where a and b (b > 0) are arbitrary constants (Toda, 1963). Without any loss of generality, we set a = 0 and b = 1 in all our analyses. Figure 1 illustrates the relationship between probability predictions and Brier scores for binary cases (where 0 = outcome does not happen in blue, and 1 = outcome does happen in red). Brier scores measure the mean square difference between the predicted probability assigned to the possible outcomes and the actual outcome. Thus, lower Brier scores indicate better calibration of a set of predictions.
Figure 1. Relationship between probability predictions and Brier scores in events with binary outcomes.
In addition to motivating forecasters (Gneiting & Raftery, 2007), these scores provide a means of assessing relative accuracy as they reflect the “quality” or “goodness” of the probabilistic forecasts: The lower the mean Brier score is for a set of predictions, the better the predictions.
Typically, scores do not take into account the characteristics of the events, or class of events, being forecast. Consider, for example a person predicting the results of games to be played between teams in a sports league (e.g., National Football League, National Basketball Association). A probability forecast, p, earns the same score if it refers to the outcome of a game between the best and worst teams in the league (a relatively easy prediction) or between two evenly matched ones (a more difficult prediction). Similarly, they give equal credit for assigning the same probabilities when predicting political races where one candidate runs unopposed (an event with almost no uncertainty) and in very close races (an event with much more uncertainty). This paper uses the Item Response Theory (IRT) framework (e.g., Embretson & Reise, 2000; Lord, 1980; van der Linden & Hambleton, 1996) to incorporate event characteristics and, in the process, provides a framework to identify superior forecasters.
IRT is a stochastic model of test performance that was developed as an alternative to classical test theory (Lord & Novick, 1968). It describes how performance relates to ability measured by the items on the test and features of these items. In other words, it models the relation between test takers’ abilities and psychometric properties of the items. One of the most popular IRT models for binary items is the 2-parameter logistic model:
| Pj (θi)= |
| (2) |
where θi is the person’s ability, aj and bj are the item discrimination and item difficulty parameters, respectively. Pj(θi) is the model’s predicted probability that a person with ability θi will respond correctly to item j with parameters aj and bj.
From this point on, we will abandon the test theory terminology and embrace the corresponding forecasting terms. We will refer to expertise, instead of ability, and events, instead of items. Extending the IRT approach to the assessment of probabilistic forecasting accuracy could bridge the measurement gap between expertise and features of the target events (such as their discrimination and difficulty) by putting them on the same scale and modeling them simultaneously. The joint estimation of person and event parameters facilitates interpretation and comparison between forecasters.
The conventional estimates of a forecaster’s expertise (e.g., his or her mean Brier score, based on all events forecast) are content dependent, so people may be assigned higher or lower “expertise” scores as a function of the events they choose to forecast. This is a serious shortcoming because (a) typically judges do not forecast all the events and (b) their choices of which events to forecast are not random. In fact, one can safely assume that they select questions strategically: Judges are more likely to make forecasts about events in domains where they believe (or are expected to) have expertise or events they perceive to be “easy” and highly predictable, so their Brier scores are likely to be affected by this self-selection that, typically, leads to overestimation of one’s expertise. Thus, all comparisons among people who forecast distinct sets of events are of questionable quality.
A remedy to this problem is to compare directly the forecasting expertise based only on the forecasts to the common subset of events forecast by all. But this approach can also run into problems. As the number of forecasters increases, comparisons may be based on smaller subsets of events answered by all and become less reliable and informative. As an example, consider financial analysts who make predictions regarding future earnings of companies that are traded on the market. They tend to specialize in various areas, so it is practically impossible to compare the expertise of an analyst that focuses on the automobile industry and another that specialize in the telecommunication area, since there is no overlap between their two areas. Any difference between their Brier scores could be a reflection of how predicable one industry is, compared to the other, and not necessarily of the analysts’ expertise and forecasting ability. An IRT model can solve this problem. Assuming forecasters are sampled from a population with some distribution of expertise, a key property of IRT models is invariance of parameters (Hambleton & Jones, 1993): (1) parameters that characterize an individual forecaster are independent of the particular events from which they are estimated; (2) parameters that characterize an event are independent of the distribution of the abilities of the individuals who forecast them (Hambleton, Swaminathan & Rogers, 1991). In other words, the estimated expertise parameters allow meaningful comparisons of all the judges from the same population as long as the events require the same latent expertise (i.e., a unidimensional assumption).
Most IRT models in the psychometric literature are designed to handle dichotomous or polytomous responses and cannot be used to analyze probability judgments, which, at least in principle, are continuous. One recent exception is the model by Merkle, Steyvvers, Mellers and Tetlock (2016). They posit a variant of a traditional one-factor model, and assume that an individual i’s observed probit-transformed forecast yij on event j is a function of the forecaster’s expertise θi:
| yij=b0j+(b1j−b0j)e−b2 tij +λj θi+eij (3) |
where tij is the time at which individual i forecast item j (measured as days until the ground truth of the event is determined), b0j reflects item j’s easiness as days to item expiration goes to infinity, b1j reflects item j’s easiness at the time the item resolves (i.e., the item’s “irreducible uncertainty”), and b2 the describes change in item easiness over time.
The underlying latent individual trait in Merkle et al.’s (2016) IRT model, θi, measures expertise, but it is not linked with a proper scoring rule. When using a model to analyze responses, it is always beneficial and desirable to have the model reflect the respondents’ knowledge about the evaluation criterion in the testing environment. In the absence of such a match, one can question the validity of the scores obtained, as it is not clear that they measure the target construct. A good analogy is a multiple-choice test that is scored with a penalty for incorrect answers without informing the test takers of the penalty (Budescu & Bar-Hillel, 1993). In this paper we propose a new model that is based on the same scoring rule that is communicated to forecasters.
More generally, we describe an IRT framework in which one can incorporate any proper scoring rule into the model, and we show how to use weights based on event features in the proper scoring rules. This leads to a model-based method for evaluating forecasters via proper scoring rules, allowing us to account for additional factors that the regular proper scoring rules rarely consider.
Consider a forecasting event j with K possible responses that is scored by a given proper scoring rule. Each response is assumed to follow a multinomial distribution with a probability of each possible response specified in equation (4, below). In most cases, each possible response links to one possible score, so an event with K possible responses, has K possible scores. Each possible score is denoted as sk where k=(1,…,K) and sk ∈ [0,1], with 0 being the best and 1 being the worst. The model’s predicted probability that the i’th (i=1,…, N) forecaster receives a score sij=sk′ based on a proper scoring rule on the j’th (j=1,…,M) event conditioning on his/her expertise θi is denoted as p(sij=sk′|θi). Proper scores in the model should match the proper scoring rule that motivates and guides the forecasters. In this paper we focus on the Brier scoring rule. The model predicts the probability via the equation
| p(sij=sk′|θi)= |
| (4) |
Here aj is the event’s discrimination parameter, bj is its difficulty parameter, defined as the event’s location on the expertise scale, and ρk is a parameter associated with the k’th (k=1, …, K) possible score. The parameter ρk is invariant across events and reflects the responses selected and their associated scores.
Figure 2. Distributions of the original probability forecasts and their rounded values
Figure 3. Item characteristic curves (varying only event difficulty b).
The model requires forecasts to be binned. Choosing a large number of bins (K) would complicate and slow down the estimation process, especially when the data are sparse (as is the case in our application, to be described in the next section). Thus, it is more practical to estimate the model with smaller values of K and we choose to set K = 6. Figure 2 shows the distribution of the probability responses that we used (see details below) in the left panel, and the distribution of the binned probabilities in the right panel. Clearly, the distribution of binned probabilities preserves the shape of the empirical distribution, so it is reasonable to assume that it contains most of the information needed to estimate the model parameters accurately. It is reasonable to assume the model would work better with more, say K = 11, bins so our results are essentially a lower bound for the quality of the method.
Figure 4. Item characteristic curves (varying only event discrimination a).
Figure 5. Item characteristic curves (varying only the scaling parameter ρ.
Some key features of the model are illustrated in Figures 3 through 5. The curves plot the relationship between expertise and the probability of giving a perfect prediction (that maps into a Brier score, sk′=6=0) to events of different difficulties bj, event discriminations aj and the scaling parameter ρk=6 of a perfect prediction. The blue curve that is replicated in all three figures represents a “baseline” event with bj = −1, aj = 3 and ρk=6 = −0.6. The values of the other five scaling parameter ρk=1,…5 are fixed in all the curves and they are (−0.02, −0.62, −0.58, −0.51, −0.56).
Figure 3 shows how the model captures event difficulty. The four curves have the same discrimination and the same level of ρk=6, but differ in event difficulty (bj). The top curves represent easier events, and the bottom curves represent harder ones. For harder events, the probability of making perfect predictions with a Brier score of 0 (sk′=6=0) is lower at all levels of expertise. The stacked positions of the four curves show that for any expertise level, the model predicts probability increases for easier events.
Figure 4 illustrates discrimination – the degree to which an event differentiates among levels of expertise. The four curves have the same difficulty level and the same values of ρk=6, but differ in discrimination, which drives their steepness. The top curves represent the most discriminating events: they are steeper than the other two, so the probability of being correct changes rapidly with increases in expertise.
Finally, Figure 5 shows the scaling parameter, ρk=6. The model treats the probability forecasts as a discrete variable: with K possible probability forecast responses, there are K possible scores. The scaling parameter is necessary to link the score to the model. In our model, each event gets its own slope and own “location” parameters, but the differences among scores around that location are constrained to be equal across event. In other words, the values of ρk are fixed across all the items. Curves in Figure 5 have the same level of discrimination and difficulty, but differ with respect to ρk=6. The pattern is similar to that in Figure 3, indicating that ρk=6 serves a similar function as event difficulty, with the difference being that the event difficulty parameter varies from event to event, while ρk=6 is fixed across all the events.
Bock’s (1972) generalized nominal response model is an unordered polytomous response IRT model. The model states that the probability of selecting the h’th category response in an item with m mutually exclusive response categories is:
| p(h)(θ ) = |
| (5) |
where ah and bh are the discrimination parameter and the difficulty parameter for the category h of the item. Our model (Equation 6) is a special case of the Bock’s model (Equation 7). The values of aj (1−sk′) and (bj+ρk′) can be re-expressed as ak′ and bk′ and we can rewrite Equation (6) accordingly:
| p(sk′|θi)= |
| (6) |
According to Fisher (1922, p. 310), a statistic is sufficient if “no other statistic that can be calculated from the same sample provides any additional information as to the value of the parameter.” The sufficient estimate of the judges’ expertise in our model is a monotonic transformation of the operational scoring rule. More specifically, in the current implementation (Equation 6), θi is a weighted sum of event-specific Brier scores for forecaster i across all events he/she forecasted (see derivation in Appendix A).
The intuition is straightforward: each event-specific Brier score is weighted by the event’s level of discrimination, so that the more (less) discriminating an event is, the more we over (under) weigh it in estimating the judge’s expertise. Thus, our main prediction is that expertise estimates from the model will be a more valid measure of the judges’ underlying forecasting expertise than the raw individual proper scores that weight all events equally.
We take a Bayesian approach (see, e.g., Gelman, Carlin, Stern & Rubin, 1995) for the estimation of model parameters. This requires specification of prior distributions for all its parameters. The prior distribution for expertise parameters, θi, was a standard normal distribution (zero mean and unit variance). For bj and ρk, we used vague normal distribution priors with a mean of 0 and standard deviations of 5. We rely on vague priors because we don’t have much prior information about the distributions of the event and the expertise parameters. We prefer to let the observed data (forecasts) find the distributions iteratively. We assume that the event discrimination parameter, aj, has a positively-truncated normal prior (Fox, 2010). Fixing this parameter to be positive makes the IRT model identifiable with respect to the location and scale of the latent expertise parameter. To summarize, the model parameters’ priors follow the Gaussian distributions with the means and variances shown below:
| θi ∼ N(0,1) aj ∼ N(0,25)∈ [0,+∞) bj ∼ N(0,25) ρk ∼ N(0,25). (7) |
We used the Just Another Gibbs Sampler (JAGS) program (Plummer, 2003) to sample posterior distribution in equation (5). JAGS is a program for analysis of Bayesian hierarchical models using Markov Chain Monte Carlo (MCMC) simulation. It produces samples from the joint posterior distribution. To check the convergence of the Markov chain to the stationary distribution1, we used two criteria: (1) Traceplots that show the value of draws of the parameter against the iteration number and allow us to see how the chain is moving around the parameter space; (2) A numerical convergence measure (Gelman & Rubin 1992) based on the idea that chains with different starting points in the parameter space converge at the point where the variance of the sampled parameter values between chains approximates the variance of the sampled parameter values within chains. A role of thumb states that the MCMC algorithm converges when the Gellman – Rubin measure is less than 1.1 or 1.2 for all parameters of the model (Gelman & Rubin 1992).
We illustrate the model by using the geopolitical forecasts collected by the Good Judgment Project (GJP) between September 2011 and July 2014 (Mellers et al. 2014; Mellers, Stone, Murray, Minster, Rohrbaugh, Bishop, Chen, Baker, Hou, Horowitz, Ungar and Tetlock, 2015; Tetlock, Mellers, Rohrbaugh and Chen, 2014). GJP recruited forecasters via various channels. Participation in the forecasting tournament required at least a bachelor’s degree and completion of a 2-hour long battery of psychological and political knowledge tests.
Participants were informed that the quality of their forecasts would be assessed using a Brier score (Brier, 1950) after the scoring was explained to them, and their goal was to minimize their average Brier score (across all events they chose to forecast). Mellers et al. (2014) provide further details about data collection. A unique feature of this project is that participants could choose which events to forecast. The average number of events forecasters predicted every year during the first three years of the tournament2 was 55. Overall there were approximately 458,000 forecasts from over 4,300 forecasters and over 300 forecasting events. The data set is very sparse, with almost 66% “missing” forecasts.
Figure 6. Observed and expected response frequencies at the global level.
We began by fitting the IRT forecasting model with the Brier scoring rule to a reduced, but dense, subset of the full GJP data set to avoid potential complications associated with missing data. This data set, created and used by Merkle et al. (2016), includes responses from 241 judges to 157 binary forecasting events). It contains responses of the most active and committed judges who made forecasts on nearly all the events. Each judge forecast at least 127 events and each event had predictions from at least 69 judges. The mean number of events forecast by a judge was 144 and the mean number of forecasts per event was 221, and the data set included 88,540 observations.3 The percentage of missing data in this data subset was only 8%. They were treated as missing at random and were not entered into the likelihood function.
The probabilistic forecasts were rounded to 6 equally spaced values (0.0, 0.2, 0.4, 0.6, 0.8 and 1.0) as shown in Figure 2. Convergence analyses show that the MCMC algorithm reached the stationary distributions, and Gelman & Rubin’s (1992) measures for all of the model’s parameters were between 1 and 1.5.4 Importantly, Gelman & Rubin’s (1992) measures for the estimated expertise parameters were all less than 1.2. The trace plots of the parameter estimates show that the chains mixed well. The trajectories of the chains are consistent over iterations and the corresponding posterior distributions look approximately normal.
Figure 7. Boxplot of the event-level correlations between the observed and the expected response frequencies.
Model Checking. We compared the observed and expected response frequencies at the global level and the event level. The observed response frequencies are, simply, the counts of each of the 6 possible probability responses. The model calculates the probability of each of the 6 possible responses (0, 0.2, 0.4, 0.6, 0.8 and 1) for each unique combination of an event and a forecaster. The expected frequencies are the sums of the model predicted probabilities for each of the 6 possible responses aggregated across all events and forecasters.
Figure 6 plots the observed and predicted response frequencies for each of the 6 possible responses across all events and respondents. The correlation between expected and observed values is 0.97. Figure 7 shows the distribution of the correlations between the expected and observed values at the event level (i.e., 157 correlations). One hundred and twenty of the 157 events (76.4%) have correlations above 0.9 and 15 of them (9.6%) have correlations between 0.7 and 0.9.
Only 22 events (14%) of the correlations between observed and the expected frequencies are below 0.7. There is no obvious commonality to these events in terms of duration5 or domain6 but their estimated discrimination parameters are lower than the others (mean of 0.3 and a standard deviation of 0.27), suggesting that they don’t discriminate among levels of expertise. Interestingly, these are disproportionately events that resolved as change from the “status quo”, as shown in Table 1.7 The odds ratio in the table is 113/19/7/13=11, and the Bayes factor in favor of the alternative that the variables are not independent is 8,938, which projects strong evidence against the null hypothesis. Results indicate that the model fits the forecasts for the status quo event better than the non-status quo events. In other words, it is harder to predict change than constancy.
Table 1. Joint distribution of resolution type and goodness of fit in 157 events
Not Classified (NC) refers to events that cannot be classified as status-quo or not.
Parameter estimates. The events in this subset were relatively “easy”8 with only 15 out of 157 (9.5%) events having positive bj estimates. The mean bj estimate was –1.37 (SD=2.70) and single event estimates ranged from –9.27 to 13.89. The mean discrimination, aj, was 2.29, and estimates ranged from 0.04 to 10.43. The mean estimated expertise, θi, was 0.04 (SD=0.96) with estimates ranging from –1.71 to 3.29. The estimated values of ρk (k=1,…6) were –0.04, –0.90, –0.86, –0.79, –0.84 and –0.88 for the score categories. The first value is distinctly different from the other five ρk (k=2,…,6).9
Figure 8. The scatterplot matrix of the event Brier scores and the event parameter estimates.
Figure 9. Scatter plot matrix of the IRT forecasting model-based expertise estimates, Merkle et al.’s (2016) expertise estimates and the Brier scores.
Table 2. Polynomial and linear regressions of the expertise estimates as a function of the mean Brier scores.
Estimate S.E. t value Pr(>|t|) 4.40 0.16 27.21 <2e-16 -17.98 0.83 -21.73 <2e-16 13.68 1.01 13.48 <2e-16 Linear Regression of Model’s Expertise Estimate (n=241) 2.50 0.11 23.77 <2e-16 -7.23 0.29 -24.59 <2e-16
Relationship between Brier scores and the model parameter estimates. Figure 8 shows the scatter plot matrix (SPLOM) of the two event-level parameters and the events’ mean Brier scores. The diagonal of the SPLOM shows histograms of the three variables, the upper triangular panel shows the correlations between row and column variables, and the lower triangular panel shows the scatter plots. We observe a negative curvilinear relationship between the discrimination parameter aj and the Brier scores, indicating that events with higher mean Brier scores tend not to discriminate well among forecasters varying in expertise. Most of the bj estimates cluster around 0, with Brier scores ranging from 0 to 0.5. Among the events with Brier scores above 0.5, there is a positive relationship between Brier scores and difficulty parameters. The correlation between the discrimination and the difficulty parameters is low (.17), as they reflect different features of the events. We regressed the events’ mean Brier scores on the two parameters – discrimination and difficulty – and their squared values. The fit is satisfactory (R2 = 0.78; F(4,152) = 131.6, p < .001), and all four predictors were significant.
Figure 9 shows a SPLOM of the model’s expertise estimates, the mean Brier scores and the expertise estimates from Merkle et al.’s (2016) model of the 241 judges. We observe a negative curvilinear relationship between the model’s expertise estimates and the mean Brier scores. Judges with high expertise estimates had lower Brier scores. Table 2 shows results of linear and polynomial regressions predicting the expertise estimates. In the linear regression, the mean Brier score was the sole predictor, and the polynomial regression also included the squared mean Brier score. The R2 values for the linear and polynomial regressions are 0.72 and 0.84, respectively, indicating that the nonlinear component increases the fit significantly (by 12%). This non-linearity reflects the fact that the model uses different weights for different events as a function of the discrimination parameters to estimate expertise, a unique feature of the IRT-based expertise estimates. The relationship between Merkle et al.’s (2016) expertise estimates and mean Brier scores is also curvilinear, but the non-linearity is not as strong as that found with model. Expertise estimates of the two IRT models are moderately positively correlated, but our estimates are more highly correlated with Brier scores than those of Merkle et al.(2016).
Figure 10. The super forecasters’ and the regular forecasters’ expertise distributions. The Y axes represent expertise estimates from our model.
Identifying expertise. At the end of every year, GJP selected the top 2% forecasters (based on their Brier scores) and placed them in elite teams of “super forecasters.” These super forecasters are over-represented in our data set (n=91, or 38%). Figure 10 shows a comparison of their expertise estimates to the other 150 regular forecasters. A two-sample t-test shows a significant difference between expertise estimates for the two groups (t=16.13, df=239, p<2.2e−16; Cohen’s d = 2.09) with the super forecasters’ expertise estimates (M=1.30, SD=0.91) being substantially higher than the regular forecasters’ (M=−0.34, SD=0.57). We ran a similar two-sample t-test on the Brier scores of the two groups and found a significant difference between the two groups (t = −11.96, df = 239, p< 2.2e−16, Cohen’s d = 1.55). The mean Brier score of the super forecasters was 0.22 with a standard deviation of 0.04, and the mean Brier score of regular forecasters was 0.38 with a standard deviation of 0.10. In other words, our expertise estimates differentiate better between the two groups than the Brier scores.
Table 3. Dominance analysis for the mean Brier score in the 4th period of the GJP tournament.
Additional contribution of: Model Predictors R2 Merkle Bo Null 0.00 0.37 0.07 0.39 Brier 0.37 . 0.00 0.04 Merkle 0.07 0.29 . 0.33 Bo 0.39 0.02 0.01 . Brier & Merkle 0.37 . . 0.05 Brier & Bo 0.41 . 0.01 . Merkel & Bo 0.40 0.02 . . All: Brier, Merkle, Bo 0.42 . . . Global Dominance 0.42 0.18 0.03 0.21 Dominance % 100.0% 42.82% 7.42% 49.76%
Table 4. Dominance analysis for the activity level in the 4th period of the GJP tournament.
Additional contribution of: Model Predictors R2 Merkle Bo Null 0.00 0.04 0.06 0.10 Brier 0.04 . 0.03 0.07 Merkle 0.06 0.01 . 0.04 Bo 0.10 0.02 0.01 . Brier & Merkle 0.07 . . 0.05 Brier & Bo 0.12 . 0.01 . Merkel & Bo 0.11 0.01 . . All: Brier, 0.12 . . . Merkle, Bo Global Dominance 0.12 0.02 0.03 0.07 Dominance % 100.00% 19.27% 25.06% 55.67%
We performed an additional test of the robustness of the expertise parameters by dividing the 157 events into 4 groups according to their closing dates. There were 39 events each in the 1st, 2nd, and 4th periods and 40 events in the 3rd period.10 We estimated the expertise parameters using both Merkle et al.’s model and our IRT forecasting model, as well as the mean Brier scores for all the 241 forecasters in each of the 4 time periods. We identified the top M performers (Ms=20,30,40,and 50) in each of the 12 cases (3 methods * 4 periods) and measured the proportion of agreement between the various classifications in the top M.11 Figure 11 plots the mean (± standard error) agreement of the two IRT based models (Bo et al. and Merkle et al.) with the Brier scores in the other periods. The ability to predict the top forecasters decreases monotonically as we become more selective and focus our attention on a smaller group of top forecasters. Most importantly for our purposes, the rate of deterioration in predictive ability is not uniform across methods: Our model is the most stable in this respect and, for M ≤ 40, it does (slightly) better than the Brier scores. Researchers generally consider Brier scores the gold standard to assessing predictions, and our model predicts the judges with best Brier scores in other periods as well, or better, than Brier scores from different periods.
Figure 11. Agreement with top Brier scores across time by the 3 methods. X axis — M represents the number of top performers; Y axis – Mean represents the mean agreement calculated based on the three methods (Bo et al., Brier Score, Merkle et al); Bars represent the standard errors.
Predicting future performance. A subset of the judges (n=130) also participated in the 4th year of the tournament (between August 2014 to May 2015), and they provided 58,888 new forecasts. We used the expertise scores, which include the IRT expertise estimates from both Merkle et al.’s model and our IRT forecasting model and the rescaled Brier scores12 of these 130 judges in years 1 to 3 to predict their mean Brier scores in year 4 and their activity level (the number of events they predicted). We used dominance analysis (Budescu, 1993; Azen & Budescu, 2003) to analyze the contribution of the three predictors – the IRT expertise estimates from Merkle et al.’s model (abbreviation: Merkle), the IRT expertise estimates from our model (abbreviation: Bo) and the rescaled Brier scores (abbreviation: Brier) – to the models.
Results are shown in Tables 3 and 4. We examine R2 or the proportion of variance accounted for in the year 4 Brier scores that is reproduced by the predictors in the model. The additional contributions of every other predictor are measured by the increase in the R2 from adding that predictor to the regression model. For example, the additional contribution of Brier in the model, where Merkle is the only predictor, is computed as the increase of Brier in R2 when Brier is added to the model (RBrier & Merkle2− RMerkle2=0.37−0.07=0.30). The global dominance is the mean of the average contribution at each model size. For example, the global dominance of “Brier” is calculated using the mean of the average contribution of model sizes of 0, 1 and 2: 0.366+0.292+0.018/2+0.016/3=0.179. As shown in Tables 3 and 4, the expertise estimated from our IRT model is the dominant predictor.
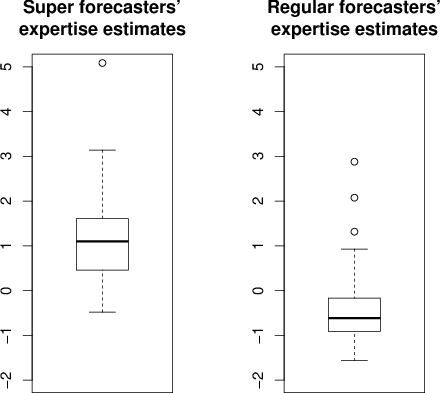
Figure 12. Super forecasters and regular forecasters’ expertise distributions. Y axes represent expertise estimates from our model.
Table 5. Correlations between true model parameters and recovered parameters for different combinations of missing mechanism and levels of missing data.
Table 6. RMSEs between true model parameters and recovered parameters for different combinations of missing mechanism and levels of missing data
We conducted several simulations to check the ability of the model (and the estimation approach) to recover the model’s parameters in the presence of large levels of missing data. In all of the simulations we used the event parameter estimates from the original analysis based on 241 judges. We simulated responses of 300 new forecasters (with expertise parameters sampled from a standard normal distribution) to the same 157 binary events. We implemented two different missing data mechanisms (missing at random/AR; and missing not at random/NAR) and simulated data sets with different levels of incompleteness (20%, 40%, 60% and 80%). Under the NAR mechanism, we generated missing responses based on the forecasters’ location in the distribution of expertise and the pre-determined degree of sparsity.13
Table 5 presents the correlations between the parameters used to simulate the responses and their recovered values. The corresponding Root Mean Squared Errors (RMSE) are shown in Table 6. In both tables, each column represents one of the 9 data sets. All the correlations are high and, as expected, they decrease, but only moderately, as a function of the rate of missing data, with only small differences between the missing data mechanisms. The values of the RMSEs also don’t change substantially from case to case, indicating that the model and the estimation algorithm tolerate both types of missing data mechanism and high degrees of sparsity.
Encouraged by the results of these simulations, we applied the IRT forecasting model with the Brier scoring rule to a larger subset of the geopolitical forecasting data collected by GJP, with more missing data. In this analysis we included all judges who forecast at least 100 events, and all events that had at least 100 forecasts. The new data set included 393 forecasters and 244 events, and has 58,16714 observations. The degree of missing data (relative to the complete data set with observations in all the unique combinations of an event and a forecaster) was 39.6%.
After 60,000 iterations, the chains converged and the Gelman & Rubin’s (1992) measures for 875 out of 887 model’s parameters were between 1 and 1.3, and for the other 15 parameters were between 1.3 and 1.6. The correlation between the observed and predicted frequencies at the global level was almost 1.00, and the mean, event-specific, correlation was 0.97 (only 29 events had correlations below 0.7).
We used the 87 common events to correlate the two sets of event parameters and obtained high correlations: cor(b1, b2)=0.93, cor(a1, a2)=0.70. We used the 205 common forecasters to compare the two sets of expertise parameters and found cor(θ1, θ2)=0.92. Expertise estimates from the model were highly correlated with Brier scores (−0.81). Both linear and polynomial regressions predicting expertise from Brier scores were estimated. The superiority of the polynomial regression (R2 = 0.76) over the linear one (R2 = 0.66) supports and reinforces the conclusion in the original analysis that the model captures specific features of the events when estimating the judges’ expertise.
Of the 393 forecasters, 126 (32%) were super forecasters. Figure 12 shows the boxplots of the expertise estimates of super forecasters and regular forecasters. The mean expertise estimate of the super forecasters (M=1.09, SD=0.88) was significantly higher than the mean estimate (M=−0.50, SD=0.58) of the regular forecasters (t=21.48, df=391, p<2.2e−16;Cohen’s d=2.17). The mean Brier score of the super forecasters is 0.20, with a standard deviation of 0.05, and the mean Brier score of the regular forecasters is 0.34 with a standard deviation of 0.10. The two-sample t-test for the forecasters’ Brier scores (t=-15.46,df=391,p < 2.2e−16; Cohen’s d=1.56). The value of Cohen’s d based on Brier scores is lower than that based on the expertise estimates, providing additional evidence of the superiority of the expertise scores.
We proposed an IRT model for probabilistic forecasting. The novel and most salient feature of the model is that it can accommodate various proper scoring rules, such that the expertise parameters estimated from the model reflect the operational scoring rule used to incentivize and motivate the forecasters. The model and estimation algorithm can also handle large number of missing data generated by different mechanisms, including non-random processes. As such, this model can be applied to many forecasting contexts, including sports, elections, meteorology, and business settings.
Summary In addition to estimating individual expertise, the model provides estimates of important information about events which traditional methods cannot easily quantify. Both the event-discrimination and event-difficulty parameters describe event features that matter to practitioners in forecasting contexts.
Event-difficulty parameters are on the same scale as expertise. Therefore, one can easily determine whether judges’ expertise corresponds to the difficulty level of the events they are expected to forecast. The event difficulty in forecasting complements the information in forecasters’ expertise: when fixing an event, the expertise parameter captures differences between forecasters in their prediction skills, whereas event difficulty captures the degree to which the same forecaster would make predictions for different events with differential accuracy.
Event-discrimination parameters help to identify events where it may be more important to seek high-expertise forecasters. Indeed, it is the critical weighting factor of the new score that differentiates it from the Brier scores. Interestingly, and reassuringly, we showed that the two event parameters correlate well but not very highly with the event Brier scores. The two event parameters generally track the event Brier scores but also capture additional aspects of the forecasters’ responses that the event Brier scores overlook. Most importantly, estimated event parameters from the proposed model portray some event characteristics better than the raw event Brier scores. For example, we observed that some events with high Brier scores are inherently unpredictable (black swans), so they have no power to differentiate better from worse forecasters. This is particularly true for items that resolve, surprisingly, or against the status quo. Unlike the Brier scores, the expertise parameters take into account differences among the events. The estimation procedure applies different weights to different events. Thus, in our view, estimated expertise parameters are more reliable and more informative than the individual mean Brier scores. Expertise parameters outperformed the Brier score counterparts in several ways. The expertise parameters differentiated better between the super and regular forecasters, and they did a better job of identifying these top performers in future contexts.
Probability forecast evaluation metric using IRT. Our forecasting model and Merkle et al.(2016)’s model are novel extensions of IRT models into the realm of probabilistic forecasting. Both models apply the IRT framework to improve the probability forecast evaluation metric but there is a fundamental difference between the two models. Our model embraces the fact that Brier scores are the forecaster evaluation metric in practice. We built an IRT model, with its sufficient statistics of the expertise estimates being the Brier scores. Our expertise estimates reflect the target construct and are more reliable than the Brier scores as the evaluation metric. The model also estimates events parameter to help practitioners to understand features of the events.
Merkle et al.(2016) introduce a novel evaluation metric that considers the fact that event difficulty changes over time, and predictions become easier as more information becomes available. Time is a complex modeling challenge. It is true that, for most events, Brier scores improve the closer we get to the event’s occurrence or to the deadline for its non-occurrence. The more diagnostic information attentive forecasters have, the easier the problem becomes. But there are Brier-score-degrading “black-swan” events that violate this rule – and make it harder to distinguish better from worse forecasters. This can happen when the time frame for the event is about to expire and the event suddenly happens – or when expectation build about the occurrence of the event and it suddenly does not happen. There are also events for which the subjective-probability judgments are quite violently non-monotonic, swinging quite high and low a number of times before the resolution is known, raising tricky questions about the criteria we should use in judging excessive volatility15.
From a statistical point of view the two models represent different approaches. Our model assumes, as most other IRT models, that difficulty and discrimination are stable characteristic of events and our parameters are, essentially, averages across all possible response times. Merkle et al’s model does not have such stable event-specific parameters. It models the time of the response and relies on measures of time-specific relative difficulty. Of course, the closer the forecaster’s response is to the time of the event’s resolution, the forecasters’ prediction tend to be more accurate and the event‘s relative difficulty decreases. In other words, Merkel et al’s time-specific parameters are absorbed into forecasters’ expertise parameters and events’ difficulty parameters in our model. In the GJP data, time varies across different combination of forecaster and event so modeling time adds extra complexity. It is hard to disentangle the interactions between time and individual forecasters as well as between time and specific events. In short, a systematic treatment of the role of time is beyond the current paper, but in the incorporation of the time component into our model remains a challenge for future work.
The methodology described here is certainly not restricted to Brier scoring and can be easily adapted to probabilistic response data sets with other scoring rules. One just has to replace (1−sk) with the appropriate scores, so that the latent trait estimates match the scoring system. The adoption of Bayesian inference provided in this paper is also flexible enough to accommodate data with complicated missing data mechanisms.
Conclusion and limitation. To conclude, the proposed IRT forecasting model provides reliable expertise estimates and helpful insights about event characteristics. The model and corresponding estimation algorithm are effective and flexible. Future work should include sensitivity analyses to select the number of bins to discretize the probability responses. Incorporating timing and the granularity of the forecast may further improve the model.
Armstrong, J. S. (2001). Principles of Forecasting: A Handbook for Researchers and Practitioners. Amsterdam: Kluwer Academic Publishers.
Azen, R., & Budescu D. V. (2003). The dominance analysis approach for comparing predictors in multiple regression. Psychological Methods, 8, 129–148.
Brier, G.W. (1950). Verification of Forecasts Expressed in Terms of Probability. Monthly Weather Review, 78, 1–3.
Bickel, J. E. (2007). Some comparisons between quadratic, spherical, and logarithmic scoring rules. Decision Analysis, 4, 49–65.
Budescu, D.V. (1993). Dominance analysis: A new approach to the problem of relative importance of predictors in multiple regression. Psychological Bulletin, 114, 542–551.
Budescu, D. V. & Bar-Hillel, M. (1993). To guess or not to guess: A decision theoretic view of formula scoring. Journal of Educational Measurement, 30, 277–292.
Embretson, S. E., & Reise, S. P. (2000). Item Response Theory for Psychologists. New York: Psychology Press.
Fisher, R.A. (1922). On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society A, 222, 309–368.
Fox, J. P. (2010). Bayesian Item Response Modeling: Theory and Applications. New York: Springer.
Gelman, A., Carlin, J.B., Stern, H.S., & Rubin, D.B. (1995). Bayesian Data Analysis. New York: Chapman and Hall.
Gelman, A., & Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences (with discussion). Statistical Science, 7, 457–511.
Gneiting, T., & Raftery, A. E. (2007). Strictly proper scoring rules, prediction, and estimation. Journal of the American Statistical Association, 102, 359–378.
Hambleton, R. K., & Jones, R. W. (1993). Comparison of classical test theory and item response theory and their applications to test development. Educational Measurement: Issues and Practice, 12, 38–47.
Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of Item Response Theory. Newbury Park, CA: Sage.
Lehner, P., Michelson, A., Adelman, L. & Goodman, A. (2012). Using inferred probabilities to measure the accuracy of imprecise forecasts. Judgment and Decision Making, 7, 728–740.
Lord, F. M. (1980). Applications of Item Response Theory to Practical Testing Problems. Mahwah, NJ: Erlbaum.
Lord, F. M., & Novick, M. R. (1968). Statistical theories of mental test scores. Reading. MA: Addison-Wesley.
Mandel, D.R., & Barnes, A. (2014). Accuracy of forecasts in strategic intelligence. Proceedings of the National Academy of Sciences, 111, 10984–10989.
Merkle, E. C., & Steyvers, M. (2013). Choosing a strictly proper scoring rule. Decision Analysis, 10, 292–304.
Merkle, E. C., Steyvers, M., Mellers, B., & Tetlock, P. E. (2016). Item response models of probability judgments: Application to a geopolitical forecasting tournament. Decision, 3, 1–19.
Mellers, B. A., Ungar, L., Baron, J., Ramos, J., Gurcay, B., Fincher, K., Scott, S. E., Moore, D., Atanasov, P., Swift, S. A., Murray, T., Stone, E. & Tetlock, P. E. (2014). Psychological strategies for winning geopolitical forecasting tournaments. Psychological Science, 25, 1106–1115.
Mellers, B. A., Stone, E., Murray, T., Minster, A., Rohrbaugh, N., Bishop, M., Chen, E., Baker, J., Hou, Y., Horowitz, M., Ungar, L., & Tetlock, P. E. (2015). Identifying and cultivating “Superforecasters” as a method of improving probabilistic predictions. Perspectives in Psychological Science, 10, 267–281.
Murphy, A. H., & Winkler, R. L. (1970). Scoring rules in probability assessment and evaluation. Acta Psychologica, 34, 273–286.
Plummer, M. (2003). JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In K Hornik, F Leisch, A Zeileis (Eds.), Proceedings of the 3rd International Workshop on Distributed Statistical Computing, Vienna, Austria. ISSN 1609-395X,
van der Linden, W. J., & Hambleton, R. K., (Eds). (1996). Handbook of Modern Item Response Theory. New York: Springer. Wallsten, T. S., & Budescu, D. V. (1983). Encoding subjective probabilities: A psychological and psychometric review. Management Science, 29, 151–173.
Winkler, R. L. (1967). The quantification of judgment: Some methodological suggestions. Journal of American Statistical Association, 62, 1105–1120.
Winkler, R. L., & Murphy, A. H. (1968). “Good" probability assessors. Journal of Applied Meteorology, 7, 751–758.
Tetlock, P.E. (2005). Expert Political Judgment: How Good Is It? How Can We Know? Princeton. NJ: Princeton University Press.
Tetlock, P.E., Mellers, B.A., Rohrbaugh, N., & Chen, E. (2014). Forecasting tournaments tools for increasing transparency and improving the quality of debate. Current Directions in Psychological Science, 23, 290–295.
Toda, M. (1963). Measurement of subjective probability distributions. Report ESD-TDR-63-407, Decision Sciences Laboratory, Electronic Systems Division, Air Force Systems Command, United States Air Force, L. G. Hanscom Field, Bedford, MA.
Consider the model as shown in Equation 6.
| p(sij=sk′|θi)= |
| . (8) |
We rewrite it using a vector rij with elements rijk′ equal to 1 if forecaster i receives score sk′ on item j, and 0 otherwise:
| (9) |
Now we write the likelihood function for θi:
| (10) |
This allows us to identify the sufficient statistics for θi as
| T(ri1,..., riM)= |
|
| [rijk′aj(1−sk′)] (11) |
Since ∑j=1M∑k′=1Krijk′aj is a known constant (assuming the item discrimination parameters are known), we may as well identify the sufficient statistics as
| T(ri1,..., riM)= |
| [aj |
| (rijk′sk′)]. (12) |
Thus, the sufficient statistics for θi in our model is a weighted sum of the item-specific Brier scores of forecaster i, weighted by the items’ discrimination values.
This research was supported by the Intelligence Advanced Research Projects Activity (IARPA) via the Department of Interior National Business Center contract number D11PC20061. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright annotation thereon.
Data for the full study are available at https://dataverse.harvard.edu/dataverse/gjp.
Disclaimer: The views and conclusions expressed herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of IARPA,DoI/NBC, or the U.S. Government.
Copyright: © 2017. The authors license this article under the terms of the Creative Commons Attribution 3.0 License.
This document was translated from LATEX by HEVEA.