Measuring Risk Literacy: The Berlin Numeracy Test

We introduce the Berlin Numeracy Test, a new psychometrically sound instrument that quickly assesses statistical numeracy and risk literacy. We present 21 studies (n=5336) showing robust psychometric discriminability across 15 countries (e.g., Germany, Pakistan, Japan, USA) and diverse samples (e.g., medical professionals, general populations, Mechanical Turk web panels). Analyses demonstrate desirable patterns of convergent validity (e.g., numeracy, general cognitive abilities), discriminant validity (e.g., personality, motivation), and criterion validity (e.g., numerical and non-numerical questions about risk). The Berlin Numeracy Test was found to be the strongest predictor of comprehension of everyday risks (e.g., evaluating claims about products and treatments; interpreting forecasts), doubling the predictive power of other numeracy instruments and accounting for unique variance beyond other cognitive tests (e.g., cognitive reflection, working memory, intelligence). The Berlin Numeracy Test typically takes about three minutes to complete and is available in multiple languages and formats, including a computer adaptive test that automatically scores and reports data to researchers (www.riskliteracy.org). The online forum also provides interactive content for public outreach and education, and offers a recommendation system for test format selection. Discussion centers on construct validity of numeracy for risk literacy, underlying cognitive mechanisms, and applications in adaptive decision support.

Keywords: risk literacy, statistical numeracy, individual differences, cognitive abilities, quantitative reasoning, decision making, risky choice, adaptive testing, Mechanical Turk.

1 Introduction

Mathematics skills are among the most influential educational factors contributing to economic prosperity in industrialized countries (Hunt & Wittmann, 2008). Accordingly, there has been considerable interest in the causes and consequences of numeracy (Huff & Geis, 1954; Paulos, 1988), which refers specifically to mathematical or quantitative literacy (Steen, 1990). The more basic levels of numeracy are concerned with the “real number line, time, measurement, and estimation” whereas higher levels focus on “an understanding of ratio concepts, notably fractions, proportions, percentages, and probabilities” (Reyna, Nelson, Ham, & Dieckman, 2009). Much of the research on numeracy has involved assessment of a wide range of mathematical skills among large and diverse samples. More recently, however, research and theory in the decision sciences has focused on a subset of numeracy that is important for informed and accurate risky decision making—i.e., statistical numeracy (Galesic, Garcia-Retamero & Gigerenzer, 2009; Lipkus, Samsa, & Rimer, 2001; Peters et al., 2006; Reyna et al., 2009).

In this paper, we use “statistical numeracy” specifically to refer to an understanding of the operations of probabilistic and statistical computation, such as comparing and transforming probabilities and proportions (Lipkus et al., 2001; Schwartz, Woloshin, Black, & Welch, 1997). These statistical aspects of numeracy are key features of risk assessment in business and engineering (Ayyub, 2003; Covello & Mumpower, 1985; Froot, Scharfstein, & Stein, 1993), and play central roles in health risk quantification and communication (Lipkus & Peters, 2009; see also Gigerenzer, Gaissmaier, Kurz-Milcke, Schwartz, Woloshin, 2007). Moreover—although risk commonly refers to many topics (e.g., variability in probability distributions; the effect of uncertainty on objectives; exposure to danger and loss; Figner & Weber, 2011; Fox & Tennenbaum, 2011; Gigerenzer, Swijtink, Porter, Daston, Beatty, Kruger, 1989)—economic and psychological theory have long held that decision making under risk is that involving known “statistical probabilities” and quantitative “probabilistic reasoning” (Knight, 1921; for a recent review see Rakow, 2010).¹ In these ways and others, statistical numeracy is one factor that gives rise to risk literacy—i.e., the ability to accurately interpret and act on information about risk.² Indeed, statistical numeracy has been shown to be a predictor of decision strategies, affective reactions, comprehension and normative choices across many risky economic, health, and consumer decisions (Banks, O’Dea, & Oldfield, 2010; Cokely & Kelley, 2009; Lipkus & Peters, 2009; Peters & Levin, 2008; Peters et al., 2006; Reyna et al., 2009).

Efforts to measure individual differences in statistical numeracy and risk literacy come primarily in three forms. Some research examines risky decisions in relation to individual differences in overall educational attainment, cognitive abilities, or cognitive styles (Frederick, 2005; Stanovich & West, 2000, 2008). Other research primarily focusing on clinical and health domains has developed a valid subjective instrument for self-reported estimations of numeracy (Galesic & Garcia-Retamero, 2010; Zikmund-Fisher, Smith, Ubel, & Fagerlin, 2007). Most common, however, is the use of objective performance measures of numeracy—i.e., psychometric tests (for a list of tests see Reyna et al., 2009; but see also Black, Nease, & Tosteson, 1995; Galesic & Garcia-Retamero, 2010; Lipkus et al., 2001; Peters et al., 2006; Schwartz et al., 1997; Weller, Dieckmann, Tusler, Mertz, Burns, & Peters, 2011).

In this paper, we review the development of the most widely used statistical numeracy instruments (Lipkus et al., 2001; Schwartz et al., 1997), examining successes and psychometric limits. We then introduce a new test of statistical numeracy and risk literacy—i.e., the Berlin Numeracy Test. The Berlin Numeracy Test can be used in multiple formats (i.e., computer adaptive, paper-and-pencil, multiple choice, single-item median-split), providing a fast, valid, and reliable tool for research, assessment, and public outreach. Specifically, we show that the new test offers unique predictive validity for comprehension of everyday risks beyond other cognitive ability and numeracy tests (e.g., cognitive reflection, working memory span, and fluid intelligence). Furthermore, we show that the Berlin Numeracy Test dramatically improves psychometric discriminability among highly-educated individuals (e.g., college students and graduates, medical professionals), across diverse cultures and different languages. We close with a discussion of construct validity, underlying mechanisms, and applications (e.g., custom-tailored, interactive, and adaptive risk communication).

1.1 Numeracy and risk literacy in educated samples

In 2001, Lipkus et al. (2001) published the numeracy test for highly-educated samples, as an extension of previous work by Schwartz et al. (1997). Lipkus et al. (2001) conducted a series of 4 studies (n = 463) on community samples of well-educated adult participants (at least 40 years of age) in North Carolina. Among other tasks, all participants answered 11 total numeracy questions including (i) one practice question, (ii) three numeracy questions taken from the work of Schwartz et al. (1997), and (iii) seven other questions (one of which had two parts) that were framed in the health domain (e.g., if the chance of getting a disease is 10% how many people would be expected to get the disease: (a) out of 100, (b) out of 1000). Two questions had multiple choice options while all others were open-ended. All questions were scored (0 or 1) with data aggregated across several studies and entered into a factor analysis, showing that a one factor solution was appropriate. Overall, results indicated that the refined test by Lipkus et al. (2001) was a reliable and internally consistent measure of high-school and college educated individuals’ statistical numeracy.

The results of Lipkus et al. (2001) were interesting for a number of reasons. First, the results provided additional evidence that even among educated US community samples some sizable proportion of individuals were likely to be statistically innumerate (e.g., 20% failed questions dealing with risk magnitude). Such findings were and continue to be important as many efforts designed to support informed and shared decision making rest on an erroneous assumption that decision-makers are numerate (or at least sufficiently statistically numerate; see also Guadagnoli & Ward P, 1998; Schwartz et al., 1997). Second, results indicated that domain framing (e.g., medical versus financial versus abstract gambles) did not necessary differentially affect test performance or comprehension. This finding indicates that various domain-specific items (e.g., items framed in terms of financial or medical or gambling risks) can provide a reasonable basis for the assessment of general statistical numeracy skills that will have predictive power across diverse domains. Overall, for nearly a decade, the Lipkus et al. (2001) test, and its predecessor from Schwartz et al. (1997) have provided relatively short, reliable, and valuable instruments that have been used in more than 100 studies on topics such as medical decision making, shared decision making, trust, patient education, sexual behavior, stock evaluations, credit-card usage, graphical communication, and insurance decisions, among many others (Lipkus & Peters, 2009).

1.2 Psychometrics

Despite its many successes and its influential role in advancing risky decision research, as anticipated by Lipkus et al. (2001), a growing body of data suggests some ways the current numeracy instrument could be improved (for an item response theory based analysis see Schapira, Walker, & Sedivy, 2009; see also Weller et al. 2011). For example, one major concern is that the Lipkus et al. test is not hard enough to adequately differentiate among the higher-performing, highly-educated individuals who are often studied (e.g., convenience samples from universities). To illustrate, in one study of college students at the Florida State University, data indicated that, although the Lipkus et al. (2001) test was a significant predictor of risky decisions, the Lipkus et al. test showed extensive negative skew with scores approaching the measurement ceiling (e.g., most participants answered more than 80% of items correctly; Cokely & Kelley, 2009; for similar results see Peters et al., 2006, 2007a, 2008; Schapira et al., 2009; and for similar patterns from physicians-in-training see Hanoch, Miron-Shatz, Cole, Himmelstein, & Federman, 2010). Another recent study using large probabilistically representative samples of the whole populations of two countries (the United States and Germany) revealed negative skew in numeracy scores even among participants from the general population (Galesic & Garcia-Retamero, 2010). Although most people are not college educated, most people in these two countries are likely to get the majority of questions right. These data suggest that most individuals tend to produce distributions of scores that are negatively skewed and are subject to measurement ceiling effects.

A second psychometric concern is that there is relatively little known about the relations between either the Lipkus et al. (2001) or Schwartz et al. (1997) numeracy test and other individual differences, such as basic cognitive abilities (Liberali, Reyna, Furlan, Stein, & Pardo, 2011). To illustrate, one might argue that statistical numeracy is a useful predictor of risky choice simply because it is correlated with measures of fluid intelligence. It is well known that tests of general intelligence, including those designed to measure fluid intelligence, are valid and reliable predictors of a wide variety of socially desirable cognitive, behavioral, occupational, and health-related outcomes (Neisser et al., 1996).³ Fluid intelligence tests such as Raven’s Standard or Advanced Progressive Matrices tend to be more time consuming yet also confer considerable benefits in terms of psychometric rigor and cross-cultural fairness (Raven, 2000). To date, however, few tests have investigated the extent to which the Lipkus et al. (2001) or Schwartz et al. (1997) instruments provide unique predictive power beyond other cognitive ability instruments either within or across cultures (Cokely & Kelley, 2009; Galesic & Garcia-Retamero, 2010; Garcia-Retamero & Galesic, 2010a, 2010b; Liberali et al., 2011; Okan, Garcia-Retamero, Cokely, & Maldonado, in press).

A third psychometric issue is that, even if numeracy is compared with other abilities, the observed measurement skew and ceiling effects will complicate comparative evaluations (e.g., intelligence v. statistical numeracy). Consider a recent study designed to investigate the extent to which each of several individual differences (e.g., executive functioning, cognitive impulsivity, numeracy) influenced decision-making competence (Del Missier, Mäntylä, & Bruine de Bruin, 2011; but see also 2010). The study found that numeracy was less related to some decision-making competencies than were measures of executive functioning or cognitive impulsivity, measured by the cognitive reflection test (Frederick, 2005). It is however possible that, at least in part, some measurement ceiling effects in numeracy scores among the college student sample could have limited differentiation of those individuals with the highest levels of numeracy. In contrast, both executive functioning and the cognitive reflection tests are known to provide discrimination even among highly-educated individuals. To be clear, our reading of the individual differences study by Del Missier et al. (2011) is that it represents precise and careful research using many of the best available methods and tools. However, the potential psychometric limits inherent in the now decade old numeracy test leave open important questions. To the extent that a numeracy instrument does not adequately or accurately estimate variation in the sub-populations of interest it is not an efficient basis for theory development or policy evaluations.

2 Test development and validation

Building on the work of Lipkus et al. (2001) and Schwartz et al. (1997) we aimed to develop a new psychometrically sound statistical numeracy test that could be used with educated and high-ability samples.⁴ Our goal was not to develop a high-fidelity comprehensive test of statistical numeracy or of its sub-skills. Rather, the goal was to develop a brief, valid, and easy-to-use instrument, with improved discriminability. Development of the Berlin Numeracy Test began with pre-testing on a pool of items including all items from both the Lipkus et al. (2001) and Schwartz et al. (1997) tests along with other items that were internally generated. Following a protocol analysis in which participants solved all numeracy problems while thinking aloud (Barton, Cokely, Galesic, Koehler, & Haas, 2009; see also Fox, Ericsson, & Best, 2011), we analyzed responses and selected 28 candidate questions for inclusion in the next stage of test development (i.e., 12 original items plus 16 new items).

2.1 Participants

We tested a community sample of 300 participants (57% women) from Berlin, Germany at the Max Planck Institute for Human Development. Participants were primarily current or former undergraduate or graduate students from the Humboldt, Free, and Technical Universities of Berlin. The mean participant age was approximately 26 years old (i.e., 25.86, SD=3.98; range=18–44). Each participant completed about six hours of testing over the course of two to three weeks in exchange for 40 euro (ca. $55).

2.2 Materials and procedure

A number of different instruments were used to provide convergent, discriminant, and criterion (predictive) validity for the Berlin Numeracy Test. All comparative instruments are listed and described in Table 1. Participants were tested in three separate phases. In phase 1, all participants were tested individually via computer and/or with the assistance of a laboratory technician as required by the particular instrument. The first testing session lasted for approximately two hours and consisted primary of cognitive ability instruments and cognitive performance tasks, including assessment of all candidate numeracy items. Note that participants only answered each candidate numeracy question once. During this session calculators were not allowed; however, participants were provided with paper and pens/pencils for notes. In phase 2, participants completed an online assessment from their home including a variety of self-report personality and other survey instruments. All participants agreed to complete the online portion of the study in one session in which they sat alone, in a quiet room. In phase 3, participants returned about two weeks after their first session and completed another two hours of testing. All participants were again tested individually via computer and/or with the assistance of a laboratory technician as required by the particular instrument/task. The final two hours of testing involved new cognitive performance tasks including a battery of everyday risky decision-making comprehension questions that served as a means of assessing predictive validity (Galesic & Garcia-Retamero, submitted; Garcia-Retamero & Galesic, in press).

2.3 Test construction and test items

Performance quartiles for all participants were assessed according to performance on all 28 candidate statistical numeracy questions (i.e., 12 questions from the Lipkus et al., 2001 set, plus 16 new questions). A subset of five questions with a 4-level tree structure was identified using the categorization tree application from the predictive modeling and forecasting software DTREG (Sherrod, 2003). The tree structure was constructed such that participants arriving at each branch of the tree had approximately a 50% probably of answering correctly/incorrectly. The test’s tree structure was subjected to cross-validation and showed less than 10% misclassification.⁵ Subsequent analyses indicated that reducing the 4-level solution to a simpler 3-level solution (i.e., removing one problem) did not affect test classification performance or validity yet reduced test-taking time (i.e., 10% reduction), increased test format flexibility (i.e., simplified paper-and-pencil format scoring), and provided improved discriminability among new samples (see “cross-cultural discriminability” below). All final Berlin Numeracy Test formats are based on the four questions used for the optimal 3-level categorization tree as follows (answers provided in each blank):

1. Out of 1,000 people in a small town 500 are members of a choir. Out of these 500 members in the choir 100 are men. Out of the 500 inhabitants that are not in the choir 300 are men. What is the probability that a randomly drawn man is a member of the choir? Please indicate the probability in percent. ___25%___

2a. Imagine we are throwing a five-sided die 50 times. On average, out of these 50 throws how many times would this five-sided die show an odd number (1, 3 or 5)? __30__ out of 50 throws.

2b. Imagine we are throwing a loaded die (6 sides). The probability that the die shows a 6 is twice as high as the probability of each of the other numbers. On average, out of these 70 throws how many times would the die show the number 6? ___20___out of 70 throws.

3. In a forest 20% of mushrooms are red, 50% brown and 30% white. A red mushroom is poisonous with a probability of 20%. A mushroom that is not red is poisonous with a probability of 5%. What is the probability that a poisonous mushroom in the forest is red? ___50%___

2.4 Test formats and scoring

Different research environments have different constraints such as computer-access, group-testing options, data-security requirements, etc. Accordingly, we designed the test to be flexible, offering multiple formats (for the multiple choice test see the “A Multiple Choice Format” section). A test format recommendation system is available online at www.riskliteracy.org. This system asks 1–4 questions (e.g., how much time is available for testing; what type of sample will you test) in order to recommend appropriate formats and provide sample materials.

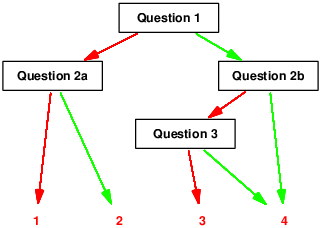
2.4.1 Computer adaptive test format

In this format, 2–3 questions (of 4 possible questions) are asked to participants (Appendix II). Questions are adaptively selected based on participants’ past success in answering previous questions (see Figure 1 for test structure). The adaptive structure means that all questions have about a 50% probability of being answered correctly with subsequent questions adjusted on the basis of participants’ prior answers. If an answer is correct/incorrect then a harder/easier question is automatically provided. A participant’s skill-level can then be determined from answers to 2–3 questions in roughly half the time normally required for the Lipkus et al. (2001) numeracy test (less than three minutes; see Table 2). To facilitate access, the computer adaptive Berlin Numeracy Test is available online in a format that automatically scores participants’ responses and reports data to researchers in terms of estimated participant quartile scores. Scores are typically batched such that the researcher requests a certain number of test scores and when that number is reached the full results are emailed. The test can be found at www.riskliteracy.org, which also provides access via other internet ready devices (e.g., smart phones). The online forum allows the public to complete the test and receive feedback on their performance relative to others, along with information about potential challenges they may face when making risky decisions. However, before completing any online test items, the adaptive test seamlessly redirects participants to a secure online server. All Berlin Numeracy Test data collection is managed and hosted via the Unipark survey software system designed for academic research (www.unipark.de). We request that researchers use the computer adaptive test format whenever possible as this format provides an efficient balance between speed and psychometric accuracy, and also allows us to continue to collect data that can be used to further refine the test.

2.4.2 Traditional (paper and pencil) format

The alternative, traditional format (Appendix III) requires that participants answer all four questions from the Berlin Numeracy Test in sequence. Scoring involves totaling all correct answers (i.e., 0–4 points possible). In this format the structure of the adaptive test is ignored, although the adaptive scoring algorithm can be applied following data collection as might be useful (e.g., to estimate quartiles compared to available norms for college educated samples). This alternative (traditional) format may be useful when computerized testing is impractical, such as in group testing or when computer access is limited. Testing requires about as long as the original Lipkus et al. (2001) numeracy test (i.e., less than 5 minutes).

2.4.3 Single-item (median) format

In cases where time is extremely limited, it is possible to use only the first item of the test (question 1) as a means of estimating median splits (Appendix IV). Those who answer the question right are estimated to belong to the top half of educated participants while all others are assigned the bottom half. Given the relatively small time savings over the adaptive format we recommend this option be avoided in favor of the computer adaptive version whenever practical. Generally, this test format takes about as long as the Schwartz et al. (1997) instrument (i.e., about 1 minute).

2.5 Results and discussion: Psychometric properties

Results of psychometric analyses are presented in Tables 2–4. Three formats of the Berlin Numeracy Test—i.e., Computer Adaptive, Traditional Paper and Pencil, and Single Item—are compared with the standard numeracy test by Lipkus et al. (2001) as well as with the brief three item test by Schwartz et al. (1997).

2.5.1 Basic attributes

In our educated sample, scores on the Lipkus et al. (2001) numeracy scale show dramatic negative skew (Table 2). Although possible scores range from 0 to 11, the lowest observed score was 5 (45% correct). Both the mean and median are close to the measurement ceiling (i.e., 88% and 91% correct, respectively). Similar levels of skew are observed for the Schwartz et al. (1997) test. In contrast, scores on the Berlin Numeracy Test are distributed evenly across the whole range of possible scores regardless of format. Estimates of internal consistency for the Berlin Numeracy Test show some modest improvement over other existing numeracy tests. However, as is common for very short tests, the Cronbach’s alpha level of all numeracy tests was below the typical .7 aspiration level.⁶ A principal axis factor analysis of the four items from the Berlin Numeracy Test indicated that all items loaded highly on a single factor explaining 45% of the observed variance. An additional study at Michigan Technological University found that, when the test was taken two different times, five days apart, it showed high levels of test-retest reliability, r(11)=.91, p=.001. All Berlin Numeracy Test formats also typically take less time to complete than the Lipkus et al. (2001) numeracy test.

2.5.2 Convergent and discriminant validity

If the Berlin Numeracy Test is successful in assessing levels of statistical numeracy, it should correlate with other numeracy tests and with measures of cognitive ability (i.e., convergent validity). Moreover, to the extent the Berlin Numeracy Test primarily measures statistical numeracy it should not correlate with essentially unrelated constructs, such as motivation, personality, beliefs, or attitudes (i.e., discriminant validity). As Table 3 shows, both requirements—high correlations with related constructs and low with unrelated constructs—are satisfied for all three forms of Berlin Numeracy Test.⁷

2.5.3 Predictive validity

One of the intended purposes of the Berlin Numeracy Test is predicting people’s understanding of information about risk in consumer, medical, and everyday contexts—i.e., predicting risk literacy. To investigate the predictive validity of the Berlin Numeracy Test, we administered a short battery of items dealing with information about everyday risks related to common consumer, health, and medical choices (e.g., evaluating the efficacy of toothpastes and cancer screenings), as well as information about probabilities typically used in weather forecasts (Garcia-Retamero & Galesic, in press; see Appendix for examples). Table 4 shows correlations of different numeracy tests with the overall accuracy of interpretations of these items. All formats of the Berlin Numeracy Test were superior to the previous numeracy tests. Both the Computer Adaptive test and the Paper and Pencil format doubled the predictive resolution of the previous tests. When either of these formats was included in the model the previous numeracy tests lost all of their unique predictive power. We next investigated the extent to which the Berlin Numeracy Test explained additional variance in risk understanding controlling for the strongest alternative predictors of performance—i.e., fluid intelligence and cognitive reflection. As Table 4 shows, all formats of the Berlin Numeracy Test explain a substantial portion of additional variance after these others tests are included in a hierarchical regression model.⁸ In contrast, both previous numeracy tests lose most (or all) of their predictive power when intelligence or cognitive reflection tests are included. Overall, results indicate that the Berlin Numeracy Test is a reliable and valid test of statistical numeracy and risk literacy, offering higher levels of discriminability and overcoming the major psychometric limitations of the Lipkus et al. (2001) test and Schwartz et al. (1997) tests.

3 Additional validation studies

3.1 Cross-cultural discriminability

The initial validation of the Berlin Numeracy Test was completed on a sample of highly-educated people living in a major metropolitan city in Germany. As a means of out-of-sample validation, we sought to assess the extent to which test discriminability generalized to other highly-educated samples from different cultures, presented in different languages. Specifically, we examined test performance in studies conducted in 15 different countries with diverse cultural backgrounds. Studies were conducted by different research groups, examining college student samples at research-active universities, primarily testing participants from introduction to psychology participant pools. Studies were conducted in China (Tsinghua University), England (University College London), France (Universite de Lausanne), Germany (Max Planck Institute for Human Development), India (Thapar University), Japan (University of Tokyo), the Netherlands (Katholieke Universiteit Leuven), Norway (University of Oslo),⁹ Pakistan (University of Punjab), Poland (Wroclaw University), Portugal (University of Porto),¹⁰ Spain (University of Granada), Sweden (Uppsala University), Switzerland (University of Basel), and the United States (Michigan Technological University).¹¹ In total, additional data from n=2685 college students was examined. All reported data are scored via the adaptive Berlin Numeracy Test algorithm, where 2–3 questions (out of 4) are used to estimate statistical numeracy quartiles for each participant.¹²

Overall results show the test generally discriminated within desirable tolerances (i.e., pm 10%) for each quartile (Table 5). Aggregating across samples, the mean test score was 51.7% correct, which closely approximated the ideal score of 50%. This score indicates that on average the first test item of the Berlin Numeracy Test achieved the intended 50% discriminability. We also observed some modest underestimation of the third quartile and commensurate overestimation in the top quartile. In part, higher top quartile scores may reflect the fact that several of our samples were collected from elite universities and selective technical/engineering universities (e.g., University College London; Tsinghua University). Visual inspection shows some specific positive and negative skewing of scores across various countries.¹³ For example, Spain, Pakistan, and India all show moderate positive skew. In contrast, the highest performing sample, which was collected in China, showed very strong negative skew. Taken together, aggregated scores closely approximated the intended quartiles. The observed distributions indicate that with only 2–3 statistical numeracy questions the Berlin Numeracy Test achieves good discriminability across most countries even when presented in different languages or when used at elite or technological universities.

3.2 Physician assistants

One goal for the Berlin Numeracy Test is to offer an instrument that can quickly assess statistical numeracy and risk literacy in highly-trained professionals. Of particular interest are those professionals who commonly make risky decisions and communicate risks. One such group in the United States is physician assistants. Physician assistants are independently licensed medical professionals who work under the supervision of physicians in all medical subspecialties (e.g., emergency medicine, family practice, surgery). Physician assistants independently diagnose and treat patients, and provide care similar to that provided by a physician, with professional training typically involving two or three years of post graduate study and clinical rotations.

Previous studies of physicians-in-training in the UK (Hanoch et al., 2010) revealed dramatic skew in responses to the Lipkus et al. (2001) test. Specifically, in one sample of physicians-in-training, Hanoch and colleagues found that the average Lipkus et al. test score was 95% correct, with 64% of participants answering all questions correctly. Here, we assessed performance of the Berlin Numeracy Test by administering a paper and pencil format to a group of physician assistant students (n = 51) who were completing their final semester of training at the University of Oklahoma.¹⁴ Results revealed slight positive skew (.16) suggesting the test was well calibrated, if somewhat difficult. A similar distribution was observed when the adaptive scoring algorithm was applied (Table 6). The mean adaptive test score was 44.3% correct, which reasonably approximated the ideal score of 50%. Note that, in contrast to other highly-educated samples, these data show some central clustering of scores. To the extent this pattern generalizes it suggests physician assistants are less likely to have very low levels of statistical numeracy, as would be expected. Overall, results indicate that the Berlin Numeracy Test is well suited for use with these and other highly-educated professionals who are often charged with interpreting and communicating risks. Ongoing research is assessing test performance among other diverse professional groups (e.g., dieticians, financial advisors, judges, lawyers, physicians, professional athletes, and poker players).

3.3 Numeracy in the general population: Data from Sweden

The Berlin Numeracy Test was designed to estimate differences in risk literacy among educated individuals. Considering the observed skew in scores from the Lipkus et al., (2001) test, the Berlin Numeracy Test may also be suitable for use among general, non-highly educated populations. As part of a larger validation and translation study, data were collected from a quota sample of adults living in the Uppsala area of Sweden (ages 20–60) who were matched against the known population on age and gender (Lindskog, Kerimi, Winman, & Juslin, 2011).¹⁵ Approximately 370 of 2000 potential participants responded to a request for participation, of which 213 were selected for testing in the current study. Of the 213 participants included in this sample approximately 30% had only high-school education with 20% completing a masters degree or higher. The test was presented in Swedish and was administered using the adaptive format. Results show the average test score was 48.8% correct, which closely approximated the theoretically ideal score of 50%. Distributions of estimated quartiles were somewhat concentrated around the middle quartiles, particularly quartile two (Table 6).

In addition to the Berlin Numeracy Data, data were also collected for the Lipkus et al., (2001) test. As expected, results showed marked skew in scores with an average score of 83.5% correct and clear negative skew (-1.94). We next compared these Lipkus et al. test scores with other data from previous studies that had been collected using probabilistic, representative sampling in the USA and Germany (Galesic & Garcia-Retamero, 2010). Results indicate that this sample of Swedish residents’ scores showed considerably more negative skew reflecting significantly higher levels of statistical numeracy compared to the populations in Germany, t (1209)=9.29, p = .001 (skewness = –.55), or the USA, t (1375) = 13.51, p = .001, (skewness = –.33).

Overall, results indicate that the Berlin Numeracy Test is well suited for estimating numeracy among some segments of the general population of Sweden or other similar community samples. However, because the current sample from Sweden is more numerate than that of either the USA or Germany, we can expect some positive skew in representative samples of the general population from the US, Germany, or other similar countries. Accordingly, when assessing statistical numeracy in representative samples of the general population we suggest including at least one other test in addition to the Berlin Numeracy Test (e.g., Weller et al., 2011). One promising strategy that adds only about 1 minute in testing time is to combine the three item Schwartz et al. (1997) test with the Berlin Numeracy Test (for an example see the next section on web panel data). Ongoing studies are examining this strategy in representative samples of residents of the USA.

3.4 United States web panel data from Mechanical Turk

Behavioral scientists are increasingly using paid web panels for data collection and hypothesis testing. One popular option for data collection is Amazon.com’s Mechanical Turk Web Panel (for a review see Paolacci, Chandler, & Ipeirotis, 2010). The first published study to assess numeracy among participants from Mechanical Turk was published in 2010 (Paolacci et al., 2010). In this study, Paolacci and colleagues assessed numeracy using the subjective numeracy scale (Fagerlin et al., 2007), which is known to correlate with the objective Lipkus et al. (2001) test (Paolacci et al., 2010). Results revealed an average subjective numeracy score of 4.35 (67% of maximum), which is similar to previously reported scores (e.g., participants recruited from a university hospital showed a modest skew (–.3); see Fagerlin et al., 2007). Similarly, we recently investigated numeracy using the Schwartz et al., (1997) test on a convenience sample from Mechanical Turk (n =250) (Okan, Garcia-Retamero, Galesic, & Cokely, in press). Consistent with results from the subjective numeracy test, results revealed moderate negative skew (-1.2), indicating an average score of 2.11 (i.e., 70% correct). A total of 42% of the sample also answered 100% of the questions correct.

To evaluate the performance of web panelists on the Berlin Numeracy Test we administered an adaptive test to a large Mechanical Turk web panel sample (n=1612). All reported data were scored via the adaptive algorithm, where 2–3 questions (out of 4) were used to estimate statistical numeracy quartiles for each participant. As anticipated, we observed positive skew (.90) in the sample scores indicating that the test was moderately difficult.¹⁶

In the previous web panel studies we observed positive and negative skew for the Berlin Numeracy Test and the Schwartz et al. (1997) test, respectively. It stands to reason that combining the two tests would yield a better distribution, providing increased discriminability. Therefore, we conducted a new study including both the Schwartz et al. test and the Berlin Numeracy Test with participants on Mechanical Turk (n=206). When scored separately, we replicated the negative (–.62) and positive (.48) skewing of scores on the two tests. However, simply adding the two scores together yielded a normal distribution with no evidence of skew (–.016). In summary, results suggest that combining the Berlin Numeracy Test with the Schwartz et al. test provides a very fast assessment (< 4 minutes) with good discriminability. This combined assessment is well suited for use with Mechanical Turk and should also be appropriate for estimating the wider range of differences in statistical numeracy that exist in samples of the general population.

3.5 A multiple choice format

In some cases researchers may require more flexibility than the current Berlin Numeracy Test formats provide. For example, many psychometric tests are given in a multiple choice format. Unfortunately, providing potential answers to participants increases the benefits of guessing. With four options, guessing would be expected to yield a score of approximately 25% correct. In contrast, in all other “fill in the blank” formats of the Berlin Numeracy Test, the contribution of a guessing parameter is essentially zero. To address this issue, multiple choice test format development began with an analysis of patterns of incorrect responses to previous tests from participants in the aforementioned Mechanical Turk study (n=1612). For each question, we listed the most frequently given incorrect options (each recorded in 8–20% of incorrect answers). Then, for each Berlin Numeracy Test question we included the correct answer, the two most frequent incorrect answers, and a “none of the above” option (Appendix V).

Next, we collected data from participants at the Michigan Technological University (n=269). Participants included convenience samples primarily from departments of Psychology, Mechanical Engineering, and Computer Science. The majority of participants were undergraduate students, with a small proportion of the sample composed of either graduate students or faculty. Participants were either sent a link asking them to complete a survey via internal listservs or tests were administered in classes. Participants were presented with one of two versions of the multiple choice format differing only in the wording of one problem (Appendix V).¹⁷ This manipulation was conducted because we received feedback that some professional groups may be more willing to participate if questions seemed related to their areas of expertise (e.g., some medical doctors will see more face validity in questions about genetic mutations as compared to choir membership). Accurate responses to the new (M=.56) v. old (M=.60) items did not significantly differ χ ² (1) = .259. Distributions of scores also did not significantly differ between tests, t(267)=1.383, p=.17, and so data sets were combined for subsequent analyses. Overall, the mean multiple choice test score was 55% correct, which reasonably approximated the ideal score of 50%. Analysis of distributions of responses indicated the multiple choice format showed no skew (–.006). Results indicate that the multiple choice format provided good discriminability and remained well balanced even when used with highly numerate individuals (e.g., computer science students).

4 General discussion

Over the last decade, the Schwartz et al. (1997) and Lipkus et al. (2001) numeracy tests have proven useful and sometimes essential for various aspects of theory development, as well as for applications in risk communication. However, as anticipated by Lipkus and colleagues, in the 10 years since publication of their test, research has identified a number of limitations and opportunities for improvement in measures of statistical numeracy. Building on the work of Lipkus et al. (2001), Schwartz et al. (1997), and many others (e.g., Peters et al., 2006, 2007b; Reyna et al., 2009), we have developed a flexible, multi-format test of statistical numeracy and risk literacy for use with diverse samples (e.g., highly-educated college graduates from around the world). Next we turn to discussion of construct validity, underlying cognitive mechanisms, and emerging applications in adaptive decision support.

4.1 Construct validity, limits, and future directions

The Berlin Numeracy Test specifically measures the range of statistical numeracy skill that is important for accurately interpreting and acting on information about risk—i.e., risk literacy. Our studies showed that a very short, adaptive numeracy test could provide sound assessment with dramatically improved discriminability across diverse samples, cultures, education levels, and languages. Content validity is clear in the types of questions included in the test—i.e., math questions involving ratio concepts and probabilities. Convergent validity was documented by showing high intercorrelations with other numeracy tests, as well as with other assessments of general cognitive abilities, cognitive styles, and education. Discriminant validity was documented by showing the test was unrelated to common personality and motivation measures (e.g., uncorrelated with emotional stability or extraversion). Criterion validity was documented by showing that the Berlin Numeracy Test provided unique predictive validity for evaluating both numeric and non-numeric information about risks. This unique predictive validity held when statistically controlling for other numeracy tests and for other general ability and cognitive-style instruments. Taken together, results converge and contribute to our evolving understanding of the construct validity of both numeracy and risk literacy.¹⁸

Going forward, more research is needed to document the causal connections between numeracy, risk literacy and risky decision making. Theoretically, improving some types of mathematics skills will improve risk literacy and risky decision making. However, the evidence of such benefits along with quantification of the magnitudes of these benefits is surprisingly limited (e.g., how much study time is required to help less numerate individuals overcome denominator neglect? Does the same level of training continue to inoculate participants under conditions of high emotional stress as might be expected in medical decisions?). As well, despite the utility of current theoretical frameworks, our understanding of underlying cognitive mechanisms is still somewhat underspecificed (for discussion see next section). Future studies are likely to benefit by more closely aligning with current research in mathematics and general literacy education, as well as research on mathematics development, mathematics expertise, and training for transfer (Seigler, 1988). Additionally, there is a need for statistical numeracy tests that provide larger item pools and parallel forms that can be administered to the same participants multiple times without inflating test scores (e.g., limiting item familiarity effects). This option for repeated measurement is necessary for the assessment of developmental changes associated with skill acquisition. Related test development efforts are currently underway for the Berlin Numeracy Test.

It is important to again note that the Berlin Numeracy Test is designed specifically for educated and highly-educated samples (e.g., college students; business, medical, and legal professionals). Discriminability will be reduced when assessing individuals who have lower levels of educational attainment (e.g., the Berlin Numeracy Test may show some positive skew in samples of high school students or among older adults). When this is a concern, researchers can include an additional instrument such as the fast three item test by Schwartz et al. (1997). The results of our Mechanical Turk web panel study show that this strategy can produce excellent discriminability with virtually no skew, estimating variation among relatively low and very high ranges of statistical numeracy.

Because the Berlin Numeracy Test provides a broad estimate of variation in statistical numeracy and risk literacy it is not able to provide a detailed assessment of specific differences in numeracy, such as identifying deficits in reasoning about probability as compared to performing multiplication. This level of analysis is necessary because, although risk literacy is a major concern, numeracy is important for thinking and general decision making well beyond its influence on risk comprehension (Peters, in press). Of note, other factor analytic research by Liberali and colleagues (2011) indicates that, at least with respect to some risky decisions and some judgments, component numeracy skills (e.g., multiplication vs. probability) can be differentially beneficial.¹⁹ We also currently do not have any theoretical account systematically linking component numeracy skills and competencies with the many various types of risky decisions people commonly face (e.g., retirement planning v. medical screening decisions, etc.). There is a need for larger scale cognitive process tracing and factor analytic assessments to be conducted across a wider range of numeracy, risk literacy, and risky decision making. Initial studies may benefit by examining relations between established numeracy tests, component math skills, and other established instruments such as the advanced decision making competency tests (Bruine de Bruin, Parker, Fischhoff, 2007; Parker & Fischhoff, 2005).

Future research will also need to use methods that provide details about the ecological frequencies of problematic risky decisions, including those related to risk literacy, using techniques such as representative sampling (Dhami, Hertwig, & Hoffrage, 2004). This type of epidemiological data could then be used to start to quantify the relative economic, personal, and social impact of specific weaknesses in numeracy and risk literacy (e.g., when and how often does denominator neglect affect high-stakes vs. lower stakes risky decisions among less numerate individuals; for a related discussion see Garcia-Retamero, Okan, & Cokely, in press). This ecological approach would provide essential input for relative prioritization of different interventions (i.e., which kind of problems do the most harm and which interventions would provide the greatest benefit; for a recent review see Reyna et al., 2009). Of course, given the wide influence of numeracy, analyses will need to be conducted across and within various domains (medicine vs. finance) and sub-domains (e.g., retirement planning versus credit decisions). Because there are many cognitive skills involved in statistical numeracy and risk literacy a test of all component skills may turn out to be prohibitively long, necessitating the use of more complex adaptive testing (Thompson & Weiss, 2011). Generally, more comprehensive assessments will also need to address the wide range of cognitive mechanisms that link numeracy, risk literacy, and decision making.

4.2 Underlying cognitive mechanisms

At its core, numeracy refers to one’s ability to represent, store, and accurately process mathematical operations (Peters, in press). As with all complex skills, individual differences in numeracy will reflect the interaction of many cognitive and affective mechanisms that vary by situation. The recent review by Reyna and colleagues (2009) provides an overview of some of the causal frameworks that are used to understand the relationship between numerical processing and risky decision making. For example, in the psychophysical tradition, theory emphasizes individual differences in the representation of internal mental magnitudes (e.g., linear v. logarithmic). In part, differences in risky decisions result from independent contributions of both evolved and acquired numerical estimation systems. That is, in part individual differences in numeracy reflect differences in one’s intuitive number sense and the affective meaning issued by this sense (Peters, in press; Peters et al., 2008; Slovic & Peters, 2006).

A second framework used to understand the relation between numeracy and risky decision making draws on fuzzy trace theory (Reyna, 2004; Reyna & Lloyd, 2006; Reyna et al., 2009). Following traditions in psycholinguistics, fuzzy trace theory explains differences in numerical processing in terms of cognitive representations and memory. Cognition is said to involve simultaneous encoding of verbatim information (“literal facts”) and gist information (“fuzzy meaning or interpretations”) into two separable forms of memory. For example, when evaluating two options with different prices, participants can be shown to encode both verbatim information (e.g., “option one costs $25 dollars and option two costs $0”) as well as gist information (e.g., “the cost is something versus nothing”). Moreover, theoretically, people have a fuzzy-processing preference such that responses tend to be based on one’s gist representation. That is, people tend to base choices on the fuzziest or the least precise representation of numeric information. There is a well developed literature linking fuzzy trace theory to judgment and decision making, including a mathematical model that explains some types of memory illusions and judgment processes. However, there is currently no validated instrument that can be used to assess or predict individual differences in one’s likelihood of relying on gist versus verbatim numeric representations.²⁰

A third framework used to understand numeracy involves computational approaches in the information processing tradition of Newell and Simon (1972), and many others (Anderson, 1982; 1996; Gigerenzer, Todd, & the ABC Research Group, 1999; Siegler, 1988). A central goal of this tradition is the development of precise, integrative computational models that allow for high-fidelity cognitive simulations (e.g., ACT-R computational models; Anderson 1996, Marewski & Mehlhorn, 2011; Schooler & Hertwig, 2005; see also Katsikopoulos & Lan, 2011). Accordingly, this tradition relies heavily on cognitive process tracing studies, including studies of reaction times, eye-tracking, information search, and think-aloud protocols (Ericsson & Simon, 1980; Schulte-Mecklenbeck, Kuhberger, & Ranyard, 2011). These methods provide data on how cognition unfolds over time, often producing relatively direct evidence about strategies (e.g., heuristics) and essential mechanisms (e.g., the influence of an incorrect understanding of math operations). Cognitive process tracing methods are also thought to be essential components of test construction and construct validation (Cronbach & Meehl, 1995; Messick, 1995). Among other virtues these methods avoid the perils of making inferences about specific cognitive processes based on averaged responses. That is, because participants sometimes use different strategies on different trials—and because different people often use different strategies—one cannot reliably identify or infer “the” underlying cognitive strategy because multiple strategies are at play (Siegler, 1987; see also Cokely & Kelley, 2009).

Although there is a considerable body of experimental research emphasizing differences in information processing, such as differences in analytical versus intuitive processing,²¹ there are only a few cognitive process tracing studies on statistical numeracy and its relationship to risky decision making (Barton, Cokely, Galesic, Koehler, & Haas, 2009). In one study of decisions in simple risky lotteries, a retrospective think-aloud protocol analysis was used in combination with assessments of decision reaction times and decision performance (Cokely & Kelley, 2009).²² Results indicated that numeracy and other abilities (e.g., working memory) predicted more normative risky decisions. However, in contrast to theory assuming that more normative decisions resulted from more normative cognitive processes (i.e., calculating expected value), numeracy was shown to predict more elaborative encoding and heuristic search (e.g., transforming probabilities, comparing relative magnitudes, and considering the time required to earn equivalent sums of money). In turn, the differences in elaborative encoding and search (e.g., reaction time) were found to fully mediate the relationship between numeracy and superior risky decision making. Similarly, individuals who score higher on general cognitive ability measures are known to spend more time preparing for tasks and more deliberatively encode task relevant information (Baron, 1978; 1990; Ericsson & Kintsch, 1995; Hertzog & Robinson, 2005; Jaeggi et al., 2011; McNamara & Scott, 2001; Sternberg, 1977; Turley-Ames & Whitfield, 2003; Vigneau, Caissie, & Bors, 2005; Jaeggi et al., 2011; see also Duckworth, Quinn, Lynam, Loeber, & Stouthamer-Loeber, 2011). Research shows that elaborative encoding causes information in working memory to be stored in long-term memory, thereby freeing-up additional resources and functionally increasing information processing capacity (Cokely, Kelley, & Gilchrist, 2006; Unsworth & Spillers, 2010). Other experimental data also shows that varying encoding and search causes changes in numerical processing and decision making performance (Natter & Berry, 2005; Smith & Windschitl, 2011). However, cognitive abilities such as numeracy do not simply result in more complex decision algorithms (Broder, 2003; Mata, Schooler, & Rieskamp, 2007). Rather, cognitive abilities tend to predict more adaptive allocation of limited cognitive resources, which tends to include more reflective, careful, and elaborative encoding even when decisions are ultimately based on heuristics (Cokely & Kelley, 2009; see also Broder, 2003; Keller et al., 2010; Mata, Schooler, & Rieskamp, 2007).

More research is needed to improve theoretical specification of how and when differences in numeracy will predict differences in encoding and search. One hypothesis is that higher levels of general abilities, including numeracy, are associated with differences in metacognition, which enables greater sensitivity to feedback (Mitchum & Kelley, 2010; see also Flavell, 1979). In turn, better detection of task feedback can give rise to more adaptive decision making as participants may become more likely to exploit cognitive niches (Marewski & Schooler, 2011). These metacognitive processes likely include a host of simple heuristics such as (i) double checking, (ii) performance predicting, and (iii) searching for disconfirming evidence—which may be useful components of reflective thinking (for a detailed theoretical account of reflective thinking, see Baron, 1985).

The link between abilities and elaborative encoding may in part explain why including the cognitive reflection test in our hierarchical model reduced the strength of the relationship between the Berlin Numeracy Test and risk comprehension (see validation study one). The predictive power of the Berlin Numeracy Test may have decreased because the cognitive reflection test captured shared-variance owing to differences in encoding and search. Research in our laboratories has demonstrated that the cognitive reflection test is sometimes uniquely associated with differences in information search, predicting differences in encoding, memory, and judgment in financial estimation tasks (Cokely, Parpart, & Schooler, 2009; in preparation). Factor analytic research by Liberali and colleagues indicates that the cognitive reflection test loads on a factor that is distinct from numeracy (Liberali et al., 2011). This cognitive reflection test factor predicted differences in one’s memory for stimulus items, which in turn was one of the strongest predictors of task performance—consistent with an elaborative encoding account.

Beyond other mechanisms, knowledge of specific mathematical operations and rules is at the heart of numeracy (Buttersworth, 2006). Research shows that major differences in skill and expert performance primarily reflect differences in knowledge and proceduralization of skill caused by differences in deliberate practice (Anderson, 1996; Ericsson, Charness, Feltovich, & Hoffman, 2006; Ericsson, Krampe, & Tesch-Römer, 1993). As with all forms of learning and expertise, skill tends to be domain-specific and generalizes or transfers only to the extent that the skill and the new task involve similar elements (Thorndike & Woodworth, 1901). For example, if a participant had an excellent working knowledge of multiplication then other tasks that involve multiplication would also benefit (e.g., risky decision tasks that require calculation of expected values). As noted, recent factor analytic research indicated that both multiplication and proportion-comprehension skills accouted for unique variance when predicting ratio biases and conjunction/disjunction fallacies (Liberali et al., 2011).

In summary, individual differences in statistical numeracy and risk literacy result from the complex interaction of many factors including one’s (1) intuitive number sense; (2) gist v. verbatim representations; (3) reflective and elaborative encoding; and (4) skilled understanding of mathematical operations. Moreover, there are likely many other important factors to consider. For example, the initial validation study for the Berlin Numeracy Test indicated that test anxiety was another factor that can be negatively related to test performance. We speculate that in some cases anxiety may reduce motivation to engage in elaborative encoding of numerical information, limiting one’s willingness to practice and develop one’s skills. However, other individuals who do not experience anxiety may instead experience higher levels of affective meaning from numbers which could inspire further encoding, reflection, and learning. In turn, greater levels of elaborative encoding and knowledge may lead to richer and more contextualized (if still imprecise) gist based representations and reasoning. Further research is needed to disentangle and map the interplay of these factors in close connection with specific task characteristics.²³

5 Conclusions

We make sense of our complex and uncertain world with data about risks that are presented in terms of ratio concepts such as probabilities, proportions, and percentages. Whether patients, consumers, and policy-makers correctly understand these risks—i.e., whether or not they are risk literate—depends in part on their statistical numeracy (see Lipkus et al., 2010 for a recent example in medicine). Rather than develop a long or comprehensive test assessing a wide-range of statistical numeracy skills, our efforts here focused on developing a fast test of statistical numeracy that leveraged available computing technology and internet accessibility (e.g., online data collection and scoring; accessible via smart phones and other internet ready devices). We believe this type of technology integration with psychometric refinement is timely given the growing need for assessment of factors that interact with risky decision-making in basic and applied domains (Cokely & Kelley, 2009; Lipkus & Peters, 2009; Galesic & Garcia-Retamero, 2010; Garcia-Retamero & Cokely, in press; Peters et al., 2006; Reyna et al., 2011).

Looking forward, there are many emerging opportunities to use this and other validated tests to enhance adaptive decision support systems (i.e., custom-tailored risk communication; Lipkus et al., 2010). For example, waiting patients or new employees selecting benefits might answer a couple of questions on a tablet computer in order to notify professionals about the appropriate level of subsequent risk discourse necessary for informed decision making. Similarly, following a diagnosis of certain diseases or the introduction of new technologies, interactive information brochures could be accessed online with custom-tailored information adaptively delivered according to one’s level of risk literacy. These instruments hold the promise of not only helping facilitate risk communication but they may also be important for mitigating legal and ethical concerns. An appropriate risk literacy test could provide additional evidence that people who are considering loans or elective surgeries have sufficient numeracy to interpret the risks in the formats that are presented. Of course, there are several promising simple solutions for transparent risk communication like visual aids and natural frequencies that are widely understandable and should be used when practical (Galesic, Garcia-Retamero, & Gigerenzer, 2009; Garcia-Retamero & Cokely, 2011; Garcia-Retamero et al., in press; Gigerenzer & Hoffrage, 1995). Nevertheless, one size cannot fit all—different situations will sometimes require different thresholds of numeracy and risk literacy for accurate understanding and informed decision making (Chapman & Lui, 2009; Gaissmaier et al., 2011).

Beyond applications in risk communication and adaptive decision support, adaptive tests like the Berlin Numeracy Test may also find use in selecting appropriate interactive tutorials for learning about risk literacy itself. Using adaptive tests can quickly get students to ability-appropriate examples of common errors in risk interpretation (e.g., confusing relative and absolute risk formats). In these cases, tests could help ensure that tutorials are not too hard or too easy, and may limit boredom and frustration. Given the importance of statistical numeracy for economic prosperity and informed citizenship even modest educational benefits may confer considerable valuable. Research on all these topics is ongoing in our laboratories along with efforts to develop other similar fast, adaptive tests (e.g., graph literacy, knowledge of sexual health risks, nutritional knowledge). Across all these endeavors, development and applications should adhere to standards for educational and psychological testing (1999). As new tools, interactive activities, and improved tests become available they will be added to the content on www.riskliteracy.org (see also Appelt, Milch, Handgraaf, & Weber, 2011; http://www.sjdm.org/dmidi).

References

Appelt, K. C., Milch, K. F., Handgraaf, M. J. J., & Weber, E. U. (2011). The Decision Making Individual Differences Inventory and guidelines for the study of individual differences in judgment and decision making. Judgment and Decision Making, 6, 252-262.

Anderson, J. R. (1982). Acquisition of cognitive skill. Psychological Review, 89, 369–403.

Anderson, J. R. (1996). The architecture of cognition. Mahwah, NJ: Lawrence Earlbaum Associates.

Ayub, B. M. (2003). Risk analysis in engineering and economics. Boca Raton, FL: Chapman & Hall/CRC press.

Buttersworth, B. (2006). Mathematical Expertise. In Ericsson K. A., Charness N., Feltovich P. J. and Hoffman R. R. (Eds.), The cambridge handbook of expertise and expert performance (pp. 553-568). New York, NY, US: Cambridge University Press.

Banks, J., O’Dea, C., & Oldfield, Z. (2010). Cognitive function, numeracy and retirement saving trajectories. The Economic Journal, 120, 381–410.

Baron, J. (1978). Intelligence and general strategies. In G. Underwood (Eds.). Strategies of information processing, (pp. 403–450). Academic Press.

Baron, J. (1985) Rationality and intelligence. New York, NY: Cambridge University Press.

Baron, J. (1990). Reflectiveness and rational thinking: Response to Duemler and Mayer (1988). Journal of Educational Psychology, 82, 391–392.

Barton, A., Cokely, E. T., Galesic, M., Koehler, A., & Haas, M. (2009). Comparing risk reductions: On the dynamic interplay of cognitive strategies, numeracy, complexity, and format. In N. A. Taatgen & H. van Rijn (Eds.), Proceedings of the 31st Annual Conference of the Cognitive Science Society (pp. 2347–2352).

Black, W. C. W., Nease, R. F. R., & Tosteson, A. N. A. (1995). Perceptions of breast cancer risk and screening effectiveness in women younger than 50 years of age. Journal of the National Cancer Institute, 87, 720–731.

Blackwell, L., Trzesniewski, K., & Dweck, C. S. (2007). Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Development, 78, 246–263.

Bors, D. A., & Stokes, T. L. (1998). Raven’s advanced progressive matrices: Norms for first-year university students and the development of a short form. Educational and Psychological Measurement, 58, 382–398.

Broder, A. (2003). Decision making with the “adaptive toolbox”: Influence of environmental structure, intelligence, and working memory load. Journal of Experimental Psychology: Learning, Memory, & Cognition, 29, 611–625.

Bruine de Bruin W. B., Parker A. M., & Fischhoff B. (2007). Individual differences in adult decision-making competence. Journal of Personality and Social Psychology, 92, 938–56.

Chapman, G. B., & Liu, J. (2009). Numeracy, frequency, and Bayesian reasoning. Judgment and Decision Making, 4, 34–40.

Cokely, E. T. (2009). Beyond generic dual processes: How should we evaluate scientific progress? PsycCritiques, 54.

Cokely, E. T., & Feltz, A. (2009a). Adaptive variation in judgment and philosophical intuition. Consciousness and Cognition, 18, 355–357.

Cokely, E. T., & Feltz, A. (2009b). Individual differences, judgment biases, and theory-of-mind: Deconstructing the intentional action side effect asymmetry. Journal of Research in Personality, 43, 18–24. DOI: 10.1016/j.jrp.2008.10.007

Cokely, E. T., & Kelley, C. M. (2009). Cognitive abilities and superior decision making under risk: A protocol analysis and process model evaluation. Judgment and Decision Making, 4, 20–33.

Cokely, E. T., Kelley, C. M., & Gilchrist, A. H. (2006). Sources of individual differences in working memory: Contributions of strategy to capacity. Psychonomic Bulletin & Review, 13, 991–997.

Cokely, E. T., Parpart, P., & Schooler, L. J. (2009). On the link between cognitive control and heuristic processes. In N.A. Taatgen & H. van Rijn (Eds.), Proceedings of the 31th Annual Conference of the Cognitive Science Society (pp. 2926-2931). Austin, TX: Cognitive Science Society.

Cokely, E. T., Parpart, P., & Schooler, L. J. (in preparation). Cognitive reflection and judgment biases. Ironic effects of fluency and memory in financial estimates.

Covello, V. T., and J. L. Mumpower. (1985). Risk analysis and risk management: A historical perspective. Risk Analysis, 2, 103–20.

Cronbach, L. J. & Meehl, P. E. (1995). Construct Validity in Psychological Tests, Psychological Bulletin, 52, 281–302.

Dhami, M. K., Hertwig, R., & Hoffrage, U. (2004). The role of representative design in an ecological approach to cognition. Psychological Bulletin, 130, 959–988.

Del Missier, F. T., Mäntylä, T., & Bruine de Bruin, W. (2010) Executive functionions in decision making: An individual differences approach. Thinking & Reasoning, 16, 69–97.

Del Missier, F. T., Mäntylä, T. & Bruine de Bruin, W. (2011). Decision-making competence, executive functioning, and general cognitive abilities. Journal of Behavioral Decision Making. DOI: 10.1002/bdm.731

Diener, E., Emmons, R. A., Larsen, R., & Griffin, S. (1985). The satisfaction with life scale. Journal of Personality Assessment, 49, 71–75.

Duckworth A. L., & Quinn P. D. (2009). Development and validation of the short grit scale (grit-s). Journal of Personality Assessment, 91, 166–174.

Duckworth, A. L., Quinn, P. D., Lynam, D. R., Loeber, R., & Stouthamer-Loeber, M. (2011). Role of test motivation in intelligence testing. Proceedings of the National Academy of Sciences, 108, 7716–7720.

Ericsson K. A., Charness N., Feltovich P. J. & Hoffman R. R. (Eds.) (2006). The cambridge handbook of expertise and expert performance. New York, NY, US: Cambridge University Press.

Ericsson, K. A., & Kintsch, W. (1995). Long-term working memory. Psychological Review, 102, 211–245.

Ericsson, K. A., Krampe, R. Th., & Tesch-R?mer, C. (1993). The role of deliberate practice in the acquisition of expert performance. Psychological Review, 100, 363-406.

Ericsson, A., Prietula, M. J., & Cokely, E. T. (2007). The making of an expert. Harvard Business Review, 85, 114–121.

Ericsson, K. A., & Simon, H. A. (1980). Verbal reports as data. Psychological Review, 87, 215–251.

Fagerlin, A., Zikmund-Fisher, B. J., Ubel, P. A., Jankovic, A., Derry, H. A., & Smith, D. M. (2007). Measuring numeracy without a math test: Development of the Subjective Numeracy Scale. Medical Decision Making, 27, 672-680.

Feltz, A., & Cokely, E. T. (2009). Do judgments about freedom and responsibility depend on who you are? Personality differences in intuitions about compatibilism and incompatibilism. Consciousness and Cognition, 18, 342–350. DOI: 10.1016/j.concog.2008.08.001.

Feltz, A., & Cokely, E. T. (in press). The philosophical personality argument. Philosophical Studies. DOI: 10.1007/s11098-011-9731-4

Figner, B., & Weber, E. U. (2011). Who takes risk when and why? Determinants of risk-taking. Current Directions in Psychological Science, 20, 211-216.

Flavell, J. H. (1979). Metacognition and cognitive monitoring: A new area of cognitive-developmental inquiry. American Psychologist, 34, 906–911.

Fox, C. R. & Tannenbaum, D. (2011). The elusive search for stable risk preferences. Frontiers in Psychology, 2, 1–4.

Fox, M. C., Ericsson, K. A., & Best, R. (2011). Do procedures for verbal reporting of thinking have to be reactive? A meta-analysis and recommendations for best reporting methods. Psychological Bulletin, 137, 316–344.

Fox, M. C., Roring, R., & Mitchum A. L. (2009). Reversing the speed-IQ correlation: Intra-individual variability and attentional control in the inspection time paradigm. Intelligence, 37, 76–80.

Frederick, S. (2005). Cognitive reflection and decision making. Journal of Economic Perspectives, 19, 25–42.

Froot, K. J., Scharfstein, D. S., & Stein, J. C. (1993). Risk management: Coordinating corporate investment and financing policies. The Journal of Finance, 48, 1629–1658.

Gaissmaier, W. & Marewski, J. N. (2011). Forecasting elections with mere recognition from lousy samples. Judgment and Decision Making, 6, 73–88.

Galesic, M., & Garcia-Retamero, R. (2010). Statistical numeracy for health: A cross-cultural comparison with probabilistic national samples. Archives of Internal Medicine, 170, 462–468.

Galesic, M., Garcia-Retamero, R., & Gigerenzer, G. (2009). Using icon arrays to communicate medical risks to low-numeracy people. Health Psychology, 28, 210–216.

Garcia-Retamero, R., & Cokely, E. T. (2011). Effective communication of risks to young adults: Using message framing and visual aids to increase condom use and STD screening. Journal of Experimental Psychology: Applied, 17, 270–328.

Garcia-Retamero, R., & Galesic, M. (Eds.) (in press). Transparent communication of risks about health: Overcoming cultural differences. New York: NY. Springer.

Garcia-Retamero, R., & Galesic, M. (2010a). How to reduce the effect of framing on messages about health. Journal of General Internal Medicine, 25, 1323–1329.

Garcia-Retamero, R., & Galesic, M. (2010b). Who profits from visual aids: Overcoming challenges in people’s understanding of risks. Social Science & Medicine, 70, 1019–1025.

Garcia-Retamero, R., Okan, Y., & Cokely, E. T. (in press). Using visual aids to improve communication of risks about health: A review. TheScientificWorld Journal.

Gigerenzer, G., Gaissmaier, W., Kurz-Milcke, E., Schwartz, L. M., Woloshin, S. (2007). Helping doctors and patients to make sense of health statistics. Psychological Science in the Public Interest, 8, 53–96.

Gigerenzer, G., Hertwig, R., van den Broek, E., Fasolo, B., & Katsikopoulos, K. (2005). A 30% chance of rain tomorrow: How does the public understand probabilistic weather forecasts? Risk Analysis, 25, 623–629.

Gigerenzer, G., & Hoffrage, U. (1995). How to improve Bayesian reasoning without instruction: Frequency formats. Psychological Review, 102, 684–704.

Gigerenzer, G., & Regier, T. (1996). How do we tell an association from a rule? Comment on Sloman (1996). Psychological Bulletin, 119, 23–26.

Gigerenzer, G., Swijtink, Z. G., Porter, T. M., Daston, L., Beatty, J., & Krüger, L. (1989). The empire of chance: How probability changed science and everyday life. New York, NY: Cambridge University Press.

Gigerenzer, G., Todd, P. M., & the ABC Group (1999). Simple heuristics that make us smart. New York, NY: Oxford University Press.

Gosling, S. D., Rentfrow, P. J., & Swann, W. B. (2003). A very brief measure of the big-five personality domains. Journal of Research in Personality, 37, 504–528.

Guadagnoli, E., & Ward, P. (1998). Patient participation in decision-making. Social Science and Medicine, 47, 329–339.

Hanoch, Y., Miron-Shatz, T., Cole, H., Himmelstein, M., & Federman, A. D. (2010). Choice, numeracy and physicians-in-training performance: The case of Medicare part D. Health Psychology, 29, 454–459.

Hertzog, C. & Robinson, A. E. (2005) Metacognition and intelligence. In O. Wilhelm, & R. W. Engle, (Eds.), Handbook of Understanding and Measuring Intelligence (pp. 101–121). CA: Sage publishers.

Hodapp, V., & Benson, J. (1997). The multidimensionality of test anxiety: A test of different models. Anxiety, Stress, and Coping, 10, 219–244.

Huff, D., & Geis, I. (1954). How to lie with statistics. New York, NY: Norton.

Hunt, E., & Wittmann, W. (2008). National intelligence and national prosperity. Intelligence, 36, 1–9.

Jaeggi, S. M., Buschkuehl, M., Jonides, J., & Shah, P. (2011). Short- and long-term benefits of cognitive training. Proceedings of the National Academy of Sciences, 108, 10081–10086. DOI: 10.1073/pnas.1103228108

Kaplan, S. & Garrick, B. J. (1981). On The quantitative definition of risk. Risk Analysis, 1, 11–27.

Katsikopoulos, K. V., & Lan, C. (2011). Herbert Simon’s spell on judgment and decision making. Judgment and Decision Making, 6, 722–732.

Keller, N., Cokely, E. T., Katsikopoulos, K., & Wegwartwh, O. (2010). Naturalistic heuristics for decision making. Journal of Cognitive Engineering and Decision Making, 4, 256–274.

Keren, G. & Schul, Y. (2009). Two is not always better than one: a critical evaluation of two-system theories. Perspectives on Psychological Science, 4, 533–550.

Knight, F. H. (1921). Risk, uncertainty and profit. Boston, MA: Houghton Mifflin Company.

Kruglanski, A. W., & Gigerenzer, G. (2011). Intuitive and deliberate judgments are based on common principles. Psychological Review, 118, 97–109.

Lang, J. W. B., & Fries, S. (2006). A revised 10-item version of the Achievement Motives Scale: Psychometric properties in German-speaking samples. European Journal of Psychological Assessment, 22, 216–224.

Liberali, J. M., Reyna, V. F., Furlan, S., Stein, L. M. & Pardo, S. T. (2011). Individual differences in numeracy and cognitive reflection, with implications for biases and fallacies in probability judgment. Journal of Behavioral Decision Making. DOI: 10.1002/bdm.752

Lindenberger, U., Mayr, U., & Kliegl, R. (1993). Speed and intelligence in old age. Psychology and Aging, 8, 207–220.

Lindskog, M., Kerimi, N., Winman, A., & Juslin, P. (2011). A Swedish validation study of the Berlin Numeracy Test. Unpublished raw data.

Lipkus, I. M., & Peters, E. (2009). Understanding the role of numeracy in health: Proposed theoretical insights. Health Education & Behavior, 36, 1065–1081.

Lipkus, I. M., Peters, E., Kimmick, G., Liotcheva, V., & Marcom, P. (2010). Breast cancer patients’ treatment expectations after exposure to the decision aid program. Adjuvant online: The influence of numeracy. Medical Decision Making, 30, 464–473.

Lipkus, I. M., Samsa, G., & Rimer, B. K. (2001). General performance on a numeracy scale among highly-educated samples. Medical Decision Making, 21, 37–44.

Marewski J. N. & Mehlhorn K. (2011). Using the ACT-R architecture to specify 39 quantitative process models of decision making. Judgment and Decision Making, 6, 439–519.

Marewski, J. N., & Schooler, L. J. (2011). Cognitive niches: An ecological model of strategy selection. Psychological Review, 118, 393–437.

Mata, R., Schooler, L. J., & Rieskamp, J. (2007). The aging decision maker: Cognitive aging and the adaptive selection of decision strategies. Psychology and Aging, 22, 796–810.

McNamara, D. S., & Scott, J. L. (2001). Working memory capacity and strategy use. Memory & Cognition, 29, 10–17.

Messick, S. (1995). Validity of psychological assessment: Validation of inferences from persons responses and performances as scientific inquiry into score meaning. American Psychologist, 50, 741–749.

Milkman, K. L., Chugh, D., & Bazerman, M. H. (2009). How can decision making be improved? Perspectives on Psychological Science, 4, 379–383.

Mitchum, A. L., & Kelley, C. M. (2010). Solve the problem first: Constructive solution strategy can influence the accuracy of retrospective confidence judgments. Journal of Experimental Psychology: Learning, Memory, and Cognition, 36, 699–710.

Natter, H. M., & Berry, D. C. (2005). Effects of presenting the baseline risk when communicating absolute and relative risk reductions. Psychology, Health & Medicine, 10, 326–334.

Neisser, U., Boodoo, G., Bouchard, T. J., Boykin, A. W., Brody, N., Ceci, S. J., Halpern, D. F., Loehlin, J. C., Perlo, R., Sternberg, R. J., & Urbina, S. (1996). Intelligence: Knowns and unknowns. American Psychologist, 51, 77–101.

Newell, A. (1973). You can’t play 20 questions with nature and win: Protective comments on the papers of this symposium. In W. G. Chase (Ed.), Visual information processing (pp. 283–308). New York, NY: Academic Press.

Newell, A. & Simon, H. A. (1972) Human problem solving. Englewood Cliffs, NJ: Prentice-Hall.

Okan, Y., Garcia-Retamero, R., Cokely, E. T., & Maldonado, A. (in press). Individual differences in graph literacy: Overcoming denominator neglect in risk comprehension. Journal of Behavioral Decision Making. DOI: 10.1002/bdm.751

Okan, Y., Garcia-Retamero, R., Galesic, M., & Cokely, E. T. (in press). When higher bars are not larger quantities: On individual differences in the use of spatial information in graph comprehension. Spatial Cognition and Computation.

Osman, M. (2004). An evaluation of dual-process theories of reasoning. Psychonomic Bulletin & Review, 11, 988–1010.

Paolacci G., Chandler, J., Ipeirotis, P. G. (2010). Running experiments on amazon Mechanical Turk. Judgment and Decision Making, 5, 411–419.

Parker A. M., Fischhoff B. (2005). Decision-making competence: external validation through an individual differences approach. Journal of Behavioral Decision Making, 18, 1–27.

Paulos, J. A. (1988). Innumeracy: Mathematical illiteracy and its consequences. New York, NY: Hill and Wang.

Peters, E. (in press). Beyond comprehension: The role of numeracy in judgment and decision making. Current Directions in Psychological Science. DOI: 10.1177/0963721411429960

Peters, E., Dieckmann, N. F., Dixon, A., Slovic, P., Mertz, C. K., & Hibbard, J. H. (2007). Less is more in presenting quality information to consumers. Medical Care Research and Review, 64, 169–190.

Peters, E., Hibbard, J. H., Slovic, P., & Dieckmann, N. F. (2007). Numeracy skill and the communication, comprehension, and use of risk and benefit information. Health Affairs, 26, 741–748.

Peters, E. & Levin, I. P. (2008). Dissecting the risky-choice framing effect: Numeracy as an individual-difference factor in weighting risky and riskless options. Judgment and Decision Making, 3, 435–448.

Peters, E., Slovic, P., Västfjäll, D., & Mertz, C. K. (2008). Intuitive numbers guide decisions. Judgment and Decision Making, 3, 619–635.

Peters, E., Västfjäll, D., Slovic, P., Mertz, C. K., Mazzocco, K., & Dickert, S. (2006). Numeracy and decision making. Psychological Science, 17, 407–413.

Rakow, T. (2010). Risk, uncertainty and prophet: The psychological insights of Frank H. Knight. Judgment and Decision Making, 5, 458–466.

Raven, J. (2000). The Raven’s Progressive Matrices: Change and stability over culture and time. Cognitive Psychology, 41, 1–48.

Reyna, V. F. (2004). How people make decisions that involve risk: A dual-processes approach. Current Directions in Psychological Science, 13, 60–66.

Reyna, V. F., & Lloyd, F. (2006). Physician decision making and cardiac risk: Effects of knowledge, risk perception, risk tolerance, and fuzzy processing. Journal of Experimental Psychology: Applied, 12, 179–195.

Reyna, V. F., Nelson, W. L., Han, P. K., & Dieckmann, N. F. (2009). How numeracy influences risk comprehension and medical decision making. Psychological Bulletin, 135, 943–973.

Schapira, M. M., Walker, C. M., & Sedivy, S. K. (2009). Evaluating existing measures of health numeracy using item response theory. Patient Educational Counseling, 75, 308–314.

Schooler, L. J., & Hertwig, R. (2005). How forgetting aids heuristic inference. Psychological Review, 112, 610–628.

Schulte-Mecklenbeck, M., Kühberger, A. & Ranyard, R. (Eds.) (2011). A Handbook of Process Tracing Methods for Decision Research: A Critical Review and User’s Guide. New York, NY: Taylor & Francis.

Schulz, E., Cokely, E. T., & Feltz, A. (2011). Persistent bias in expert judgments about free will and moral responsibility: A test of the expertise defense. Consciousness and Cognition, 20, 1722–1731. DOI: 10.1016/j.concog.2011.04.007

Schwartz, B., Ward, A., Monterosso, J., Lyubomirsky, S., White, K., & Lehman, D. R. (2002). Maximizing versus satisficing: Happiness is a matter of choice. Journal of Personality and Social Psychology, 83, 1178–1197.

Schwartz, L. M. L., Woloshin, S. S., Black, W. C. W., & Welch, H. G. H. (1997). The role of numeracy in understanding the benefit of screening mammography. Annals of Internal Medicine, 127, 966–972.

Schwarzer, R., & Jerusalem, M. (1995). Generalized self-efficacy scale. In J. Weinman, S. Wright, & M. Johnston (Eds.), Measures in health psychology: A user’s portfolio. Windsor, UK: Nfer-Nelson.

Sherrod, P. H. (2003). DTREG: Predictive Modeling Software. Software available at http://www.dtreg.com.

Siegler, R. S. (1987). The perils of averaging data over strategies: An example from children’s addition. Journal of Experimental Psychology General, 116, 250–264.

Siegler, R. S. (1988). Strategy choice procedures and the development of multiplication skill. Journal of Experimental Psychology: General, 117, 258–275.

Slovic, P., & Peters, E. (2006). Risk perception and affect. Current Directions in Psychological Science, 15, 322–325.

Smith, A. R., & Windschitl, P. D. (2011). Biased calculations: Numeric anchors influence answers to math equations. Judgment and Decision Making, 6, 139–146.

Stanovich, K. E., & West, R. F. (2000). Advancing the rationality debate. Behavioral and Brain Sciences, 23, 701–726.

Stanovich, K. E., & West, R. F. (2008). On the relative independence of thinking biases and cognitive ability. Journal of Personality and Social Psychology, 94, 672–695.

Sternberg, R. J. (1977). Intelligence, information processing, and analogical reasoning: The componential analysis of human abilities. Oxford, England: Lawrence Erlbaum.

Steen L. A. (1990). On the shoulders of giants: New approaches to numeracy. Washington, DC, US: National Academy Press.

Thompson, N. A., & Weiss, D. J. (2011). A framework for the development of computerized adaptive tests. Practical Assessment, Research, and Evaluation, 16(1). http://www.pareonline.net/pdf/v16n1.pdf.

Turley-Ames, K. J., & Whitfield, M. M. (2003). Strategy training and working memory task performance. Journal of Memory & Language, 49, 446–468.

Turner, M. L., & Engle, R. W. (1989). Is working memory capacity task dependent? Journal of Memory and Language, 28, 127–154.

Unsworth, N., & Spillers, G.J. (2010). Working memory capacity: Attention, memory, or both? A direct test of the dual-component model. Journal of Memory and Language, 62, 392–406.

Vigneau, F., Caissie, A. F., & Bors, D. A. (2005). Eyemovement analysis demonstrates strategic influence on intelligence. Intelligence, 34, 261–272.

Weller, J. A., Dieckmann, N., Tusler, M., Mertz, C. K., Burns, W., & Peters, E. (2011). Development and Testing of an Abbreviated Numeracy Scale: A Rasch Analysis Approach. Unpublished manuscript.

Zikmund-Fisher, B., Smith, D. M., Ubel, P. A., & Fagerlin, A. (2007). Validation of the subjective numeracy scale: Effects of low numeracy on comprehension of risk communications and utility elicitations. Medical Decision Making, 27, 663–671.

Appendix I: Example of everyday risky decision-making

Weather forecasting (from Gigerenzer, Hertwig, van den Broek, Fasolo, & Katsikopoulos, 2005)

Imagine there is a 30% chance of rain tomorrow. Please indicate which of the following alternatives is the most appropriate interpretation of the forecast.

Example 2: Everyday risky decision-making

Zendil—50% reduction in occurrence of gum inflammation. Zendil is a new toothpaste to prevent gum inflammation. Half as many people who used Zendil developed gum inflammation when compared to people using a different toothpaste.

Which one of the following would best help you evaluate how much a person could benefit from using Zendil?

Appendix II: Adaptive Berlin Numeracy Test format

Go to www.riskliteracy.org for a unique link to a secure adaptive test that can be embedded in your experiment and will automatically score responses. Alternatively, you can program your own adaptive test as follows:

Instructions: Please answer the questions that follow. Do not use a calculator but feel free to use the scratch paper for notes.

Appendix III: Berlin Numeracy Test traditional paper and pencil format

Instructions: Please answer the questions below. Do not use a calculator but feel free to use the space available for notes (i.e., scratch paper).

Appendix IV: Berlin Numeracy Test single item (median) format

Instructions: Please answer the questions below. Do not use a calculator but feel free to use the space available for notes (i.e., scratch paper).

Appendix V: Berlin Numeracy Test multiple choice format

Instructions: Please answer the questions below. Do not use a calculator but feel free to use the space available for notes (i.e., scratch paper).

Department of Cognitive and Learning Sciences, Michigan Technological University. Email: ecokely@mtu.edu

Center for Adaptive Behavior and Cognition, Max Planck Institute for Human Development.

Perceptual and Brain Sciences, University College London.

Department of Cognitive and Learning Sciences, Michigan Technological University.

We are indebted to the following researchers who provided assistance with cross cultural and other data collection/analysis/suggestions: Adrien Barton, Nicolai Bodemer, Gregor Caregnato, Siegfried Dewitte, Rob Hamm, Deak Helton, Stefan Herzog, Anna Koehler, Marcus Lindskog, Hitashi Lomash, Nico Mueller, Yasmina Okan, Robert Pastel, Ellen Peters, Jing Qian, Samantha Simon, Helena Szrek, Masanori Takezawa, Karl Teigen, Jan Woike, and Tomek Wysocki. We offer special thanks to Jonathan Baron. We also thank Gerd Gigerenzer, Lael Schooler, and other members of the Center for Adaptive Behavior and Cognition and of the Harding Center for Risk Literacy at the Max Planck Institute for Human Development for support and feedback. This study was part of the grant “How to Improve Understanding of Risks about Health (PSI2008–02019),” and “Helping Doctors and Their Patients Make Decisions about Health (PSI2011–22954)” funded by the Ministerio de Ciencia e Innovación (The Spanish Ministry of Science and Innovation).

On Knight’s (1921) view, risk refers to known (objective) probabilities whereas uncertainty refers to unknown, subjective or indeterminable probabilities. For a related quantification of risk that is more inclusive of both uncertainty and other decision making trade-offs related to risk management see Kaplan and Garrack (1981).

Risk literacy should not be confused with risk awareness or risk knowledge, which refer more specifically to one’s awareness of “facts” about risks (e.g., being aware that flying is safer than driving).

The underlying cognitive mechanisms that give rise to these effects are debated and remain unclear (Cokely, Kelley, & Gichrist, 2006; Ericsson, Prietula, & Cokely, 2007; Fox, Roring, & Mitchum, 2009; Neisser et al., 1996)

The Berlin Numeracy Test is named to reflect the international, interdisciplinary development effort initiated in 2007 in the Center for Adaptive Behavior and Cognition at the Max Planck Institute for Human Development. For additional discussion and similar public outreach efforts concerning expertise, ethics and philosophical judgment see philosophicalcharacter.org (Feltz & Cokely, 2009, in press; Schulz, Cokely, & Feltz, 2011).

Although some misclassification is unavoidable, the algorithm rarely misclassified a participant by more than one quartile. The assessment is similar to an item response theory analysis in that it identifies items with high levels of discriminability across the range of item difficulty with a guessing parameter of zero.

For comparison, the 3 item Cognitive Reflection Test (Frederick, 2005) had a Cronbach’s alpha =.62 and a mean duration 2.5 minutes.

For comparison, the correlation of the Cognitive Reflection Test (Frederick, 2005) with Raven’s Adv. Matrices was .40, with Vocabulary .28, and with Working Memory Span .26. Correlation with Extraversion was –.14, with Openness to experience –.23, and with Text Anxiety –.13. Correlations with other variables were not significant.

For comparison, risk comprehension was predicted by the Cognitive Reflection Test with a standardized beta of .31 and by the Raven’s test with a standardized beta of .20. When controlling for the Berlin Numeracy Test, the cognitive reflection test continued to predict unique variance .20, but Raven’s test did not .05. See the general discussion for a theoretical account of these differences.

Data collection in Norway used the traditional 4 item rather than adaptive form of the Berlin Numeracy Test. Data reported in the table are calculated using the adaptive scoring algorithm, which was highly correlated with overall score, r(154)=.90. In the standard format the average score was 62% correct showing modest skew (–.29).

Data collection in Portugal used a modified Berlin Numeracy Test. Data were only available for the single item test and are not presented in the table. Overall 46.4% of participants (n = 306) from Portugal answered the first question right (theoretical ideal test score = 50%).

We thank Nicolai Bodemer, Siegfried Dewitte, Stefan Herzog, Marcus Lindskog, Hitashi Lomash, Yasmina Okan, Jing Qian, Samantha Simon, Helena Szrek, Masanori Takezawa, Karl Teigen, Jan Woike, and Tomek Wysocki for assistance with cross cultural data collection.

Translation involved iterative cycles of back-translation with revision.

The Berlin Numeracy Test estimates quartiles, so caution is required when interpreting standard assessments of skew.

This research was financed by the Swedish Research Council. We thank Marcus Lindskog and colleagues for sharing these data.

To the extent our data generalize, results suggest that our single question 2a may allow for a rough approximation of a median split among Mechanical Turk participants.

The exact wording of the alternative question is as follows: “Out of 1,000 people in a small town, 500 have a minor genetic mutation. Out of these 500 who have the genetic mutation, 100 are men. Out of the 500 inhabitants who do not have the genetic mutation, 300 are men. What is the probability that a randomly drawn man has the genetic mutation?”

According to Cronbach and Meehl’s (1955) review of construct validity “a construct is some postulated attribute of people, assumed to be reflected in test performance.” Similarly, contemporary views hold that construct validity “…is not a property of the test or assessment as such, but rather of the meaning of the test scores” which is established by integrating and evaluating multiple lines of evidence (Messick, 1995).

The factor structures varied across two studies, which complicates interpretation although the results are suggestive.

An instrument is currently in the initial stages of development in Valerie Reyna’s Lab (personal communication with Valerie Reyna).

Although generic dual process theory is popular among decision scientists we do not discuss this framework here as there is concern about its construct validity. Arguments hold that, although it is a useful organizational framework, the framework suffers from theoretical and conceptual under-specification and inconsistency, and as a result lacks predictive validity (Cokely, 2009; Keren & Schul, 2010; Kruglanski & Gigerenzer, 2011; Gigerenzer & Regier, 1996; Osman, 2004; Newell, 1973; Reyna et al., 2009). For a brief review of recent debiasing studies see Milkman, Chugh, and Bazerman, (2009).

In concurrent verbal protocol analysis participants are asked to verbalize their thoughts while performing a task. A meta-analysis indicated that when used with the standard instructions, and Level 1 data, concurrent reports are not reactive, meaning they do not interact with cognitive processes although they may increase total processing time (Fox et al. 2011). In retrospective protocol analysis participants are asked to verbalize their thoughts after a task is complete, which can be less reliable than concurrent methods, and so converging methods such as reaction time or eye-tracking are advisable.

The information processing tradition typically takes a “systems” perspective recognizing the importance of the interaction between task environments and the computational capabilities of the actor (Simon, 1990). In other words, cognitive performance is the product of the interaction of persons, processes, and task environments (Cokely & Feltz, 2009a; 2009b; Cokely & Kelley, 2009).

Measure	Description	Reference
Fluid Intelligence (RAPM)	Short form Raven’s Advanced Progressive Matrices—a 12 item test of fluid intelligence.	Bors and Stokes (1998)
Cognitive Reflection (CRT)	The Cognitive Reflection Test uses three math questions to assess cognitive impulsivity.	Frederick (2005)
Crystallized Intelligence (Vocabulary)	A 37 item “spot-a-word” German vocabulary test.	Lindenberger, Mayr, and Kliegl (1993)
Working Memory Capacity (Span)	A multi-item performance measure of one’s ability to control attention when simultaneously solving math operations and remember words.	Turner and Engle (1989)
Understanding everyday risks	A five item battery involving interpretation of information about risks in consumer products, medical treatments, and weather forecasts.	Garcia-Retamero and Galesic (in press)
Maximizing- Satisficing	A 13 item scale measuring one’s tendency to maximize v. satisfice during decision making.	Schwartz et al. (2002)
Persistence	The Grit-S is an eight item brief measure designed to assess persistence in the face of adversity.	Duckworth and Quinn (2009)
Achievement Motivation	The AMS-R is a 10 item trait assessment of one’s general achievement motivation (e.g., one’s desire to achieve good grades or performance evaluations).	Lang and Fries (2006)
Self efficacy	A10 item self-report measure of one’s general sense of self efficacy.	Schwarzer and Jerusalem (1995)
Personality	A 10 item assessment of the Big Five personality traits.	Gosling, Rentfrow, and Swann (2003)
Test Anxiety	The TAI-G is a 20 item assessment of test-taking anxiety.	Hodapp and Benson (1997)
Implicit theories	A four item measurement of the extent to which one believes intelligence is stable v. changeable.	Blackwell,Trzesniewski, and Dweck (2007)
Satisfaction with life	A five item instrument measuring self-reported levels of one’s satisfaction with life.	Diener, Emmons, Larsen, & Griffin (1985)

	Schwartz et al. (1997), 3 items	Lipkus et al. (2001), 11 items	Berlin Numeracy Test
			Computer Adaptive Test format, 2–3 items	Paper and Pencil format, 4 items	Single Item format
Basic attributes
Range of possible scores	0–3	0–11	1–4	0–4	0–1
Range of achieved scores	0–3	5–11	1–4	0–4	0–1
Average score
Mean	2.4	9.7	2.6	1.6	.52
Median	3	10	3	2	1
Standard deviation	.82	1.38	1.13	1.21	.50
Length
Number of items	3	11	2–3	4	1
Mean duration in minutes	1.2	4.5	2.6	4.3	1.1
Reliability
Cronbach’s alpha	.52	.54	–^a	.59	–^a
Discriminability
Item % correct (mean)	.82	.89	–^b	.41	.52
Mean score of
1^st quartile	0.8	7.3	1.0	0.0	0.0
2^nd quartile	2.0	9.0	2.0	1.0
3^rd quartile	3.0	10.0	3.0	2.0	1.0
4^th quartile	3.0	11.0	4.0	3.3
^aCronbach’s alpha cannot be computed. Principal component analysis indicates that the four items used in Berlin Numeracy Test all loaded highly on a single factor explaining 45% of variance.
^bApproximately 50%, conditional on previous responses.

	Schwartz et al. (1997), 3 items	Lipkus et al. (2001), 11 items	Berlin Numeracy Test
			Computer Adaptive Test format, 2–3 items	Paper and Pencil format, 4 items	Single Item format
Convergent validity
Numeracy tests
Lipkus et al. 11 items	.75**
BNT: Computer Adaptive	.45**	.49**
BNT: Paper and Pencil	.50**	.50**	.91**
BNT: Single Item	.39**	.42**	.90**	.75**
Cognitive abilities/styles
Raven’s Adv. Matrices	.41**	.37**	.48**	.53**	.41**
Cognitive Reflection Test	.40**	.41**	.51**	.56**	.41**
Vocabulary Spot-a-word	.25**	.21**	.24**	.25**	.22**
Working memory span	.14*	.11	.21**	.20**	.16**
Discriminant validity
Motivation measures
Maximizing-Satisficing	.01	.04	.05	.04	.05
Persistence (Grit-S)	.02.	.03	–.05	–.07	–.03
Achievement motivation	–.08	–.10	–.02	.00	–.01
Self-efficacy	.00	–.01	–.01	.02	.03
Personality Traits
Emotional stability	–.10	–.05	.01	.05	–.02
Conscientiousness	–.09	–.04	–.09	–.08	–.06
Agreeableness	–.03	–.07	–.14*	–.08	–.17**
Extraversion	–.07	–.06	–.05	–.05	–.06
Openness to experience	–.14*	–.16**	–.18**	–.14*	–.16**
Other measures
Test anxiety	–.15*	–.16*	–.12	–.16*	–.09
Implicit theories	–.15*	–.13**	–.07	–.10*	–.04
Satisfaction with life	.14*	.08	.12	.16	.07
p=.05; *p<.01.

	Schwartz et al. (1997), 3 items	Lipkus et al. (2001), 11 items	Berlin Numeracy Test
			Computer Adaptive Test format, 2–3 items	Paper and Pencil format, 4 items	Single Item format
Mean proportion correct answers on understanding of everyday risks, by test quartiles
1^st quartile	.72	.68	.68	.66	.70
2^nd quartile	.74	.66	.70	.70
3^rd quartile	.78	.78	.74	.78	.78
4^th quartile	.78	.78	.84	.84
Predictive validity for correct answers on understanding of everyday risks (standardized beta coefficients)
As a single predictor	.20**	.20**	.29**	.34**	.25**
With Raven	.14*	.15*	.24**	.31**	.19**
With CRT	.09	.08	.17**	.23**	.14*
* p<.05; **p<.01

Sample	N	1st quartile	2nd quartile	3rd quartile	4th quartile
Graduating US Physician Assistants	51	.16	.39	.29	.16
Population Sample in Sweden	213	.20	.36	.24	.20
USA Web Panel Sample (M-Turk)	1,612	.49	.27	.12	.13
Total	1,876	.28	.34	.22	.16

Country	Language	N	1st quartile	2nd quartile	3rd quartile	Top quartile
China	English	166	.04	.07	.14	.75
Poland	Polish	205	.14	.20	.22	.44
England	English	420	.20	.31	.14	.35
Japan	Japanese	63	.06	.36	.24	.34
Sweden	Swedish	47	.21	.28	.17	.34
France	French	86	.30	.13	.23	.34
USA	English	55	.20	.29	.20	.31
Switzerland	German	503	.26	.23	.23	.28
Germany	German	173	.29	.21	.22	.28
Norway	Norwegian	156	.25	.24	.25	.26
Belgium	Dutch	50	.30	.30	.16	.24
India	English	83	.19	.52	.08	.21
Pakistan	English	114	.29	.41	.19	.11
Spain	Spanish	258	.48	.41	.07	.04
Total		2,379	.23	.28	.18	.31

Measuring Risk Literacy: The Berlin Numeracy Test

Edward T. Cokely* # Mirta Galesic,# Eric Schulz# % Saima Ghazal Rocio Garcia-Retamero

1 Introduction

1.1 Numeracy and risk literacy in educated samples

1.2 Psychometrics

2 Test development and validation

2.1 Participants

2.2 Materials and procedure

2.3 Test construction and test items

2.4 Test formats and scoring

2.4.1 Computer adaptive test format

2.4.2 Traditional (paper and pencil) format

2.4.3 Single-item (median) format

2.5 Results and discussion: Psychometric properties

2.5.1 Basic attributes

2.5.2 Convergent and discriminant validity

2.5.3 Predictive validity

3 Additional validation studies

3.1 Cross-cultural discriminability

3.2 Physician assistants

3.3 Numeracy in the general population: Data from Sweden

3.4 United States web panel data from Mechanical Turk

3.5 A multiple choice format

4 General discussion

4.1 Construct validity, limits, and future directions

4.2 Underlying cognitive mechanisms

5 Conclusions

References

Appendix I: Example of everyday risky decision-making

Weather forecasting (from Gigerenzer, Hertwig, van den Broek, Fasolo, & Katsikopoulos, 2005)

Example 2: Everyday risky decision-making

Appendix II: Adaptive Berlin Numeracy Test format

Appendix III: Berlin Numeracy Test traditional paper and pencil format

Appendix IV: Berlin Numeracy Test single item (median) format

Appendix V: Berlin Numeracy Test multiple choice format

Edward T. Cokely^* ^# Mirta Galesic,^# Eric Schulz^# ^% Saima Ghazal Rocio Garcia-Retamero